Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì CM là tiếp tuyến của (A)
=> \(CM\perp AM\)
=> ^CMA = 90o
=> M thuộc đường tròn đường kính AC
Vì ^CHA = 90o
=> H thuộc đường tròn đường kính AC
Do đó : M và H cùng thuộc đường tròn đường kính AC
hay 4 điểm A,C,M,H cùng thuộc đường tròn đường kính AC
b, Vì AM = AH ( Bán kính)
CM = CH (tiếp tuyến)
=> AC là trung trực MH
=> \(AC\perp MH\)tại I
Xét \(\Delta\)AMC vuông tại M có MI là đường cao
\(\Rightarrow MA^2=AI.AC\)(Hệ thức lượng)
c, Vì CM , CH là tiếp tuyến của (A)
=> AC là phân giác ^HAM
=> ^HAC = ^MAC
Mà ^HAC + ^HAB = 90o
=> ^MAC + ^HAB = 90o
Ta có: ^BAD + ^BAC + ^CAM = 180o (Kề bù)
=> ^BAD + 90o + ^CAM = 180o
=> ^BAD + ^CAM = 90o
Do đó ^BAD = ^BAH (Cùng phụ ^CAM)
Xét \(\Delta\)BAD và \(\Delta\)BAH có:
AB chung
^BAD = ^BAH (cmt)
AD = AH (Bán kính (A) )
=> \(\Delta BAD=\Delta BAH\left(c.g.c\right)\)
=> ^ADB = ^AHB = 90o
\(\Rightarrow BD\perp AD\)
=> BD là tiếp tuyến của (A)
Làm đc đến đây thôi :(

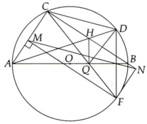
a, Tứ giác BDQH nội tiếp vì B D H ^ + B Q H ^ = 180 0
b, Vì tứ giác ACHQ nội tiếp =>
C
A
H
^
=
C
Q
H
^
Vì tứ giác ACDF nội tiếp => C A D ^ = C F D ^
Từ đó có C Q H ^ = C F D ^ mà 2 góc ở vị trí đồng vị => DF//HQ
c, Ta có H Q D ^ = H B D ^ (câu a)
H B D ^ = C A D ^ = 1 2 s đ C D ⏜
C A D ^ = C Q H ^ (ACHQ cũng nội tiếp)
=>
H
Q
D
^
=
H
Q
C
^
=> QH là phân giác
C
Q
D
^
Mặt khác chứng minh được CH là phân giác góc Q C D ^
Trong tam giác QCD có H là giao của ba đường phân giác nên H là tâm đường tròn nội tiếp => H cách đều 3 cạnh CD, CQ, DQ
d, Vì CMFN là hình chữ nhật nên MN và CF cắt nhau tại trung điểm của mỗi đường.
Trong tam giác FCD có MN//CD và MN đi qua trung điểm CF nên MN đi qua trung điểm DF
Mặt khác AB đi qua trung điểm của DF nên 3 đường thẳng MN, AB, DF đồng quy
bạn giải thích lại giúp mình câu b được không ạ? tại mình không hiểu câu đó lắm, mình cảm ơn!

a/ Ta có
\(BE\perp AC\Rightarrow\widehat{AEB}=90^o\)
\(AH\perp BC\Rightarrow\widehat{AHB}=90^o\)
=> E và H cùng nhìn AB dưới 1 góc bằng 90 độ => E;H,A;B thuộc đường tròn bán kính = \(\frac{AB}{2}\) , tâm là trung điểm AB
b/ Ta có
\(\widehat{DBE}=\widehat{DFE}\) (Góc nội tiếp đường tròn tâm O cùng chắn cung DE)
\(\widehat{DBE}=\widehat{AHE}\) (Góc nội tiếp đường tròn ngoại tiếp HBAE cùng chắn cung AE)
\(\Rightarrow\widehat{DFE}=\widehat{AHE}\) => DF//AH (Hai đường thẳng bị cắt bởi đường thẳng thứ 3 tạo thành hai góc ở vị trí đồng vị bằng nhau thì chúng // với nhau)
Mà \(AH\perp BC\Rightarrow DF\perp BC\)
c/
Từ E dựng đường thẳng vuông góc với BC cắt (O) tại I => gia của BC với EI là trung điểm EI (đường kính vuông góc với dây cung thì chia đôi dây cung) => I là điểm đối xứng E qua BC.
Nối I với H, D với H
Xét \(\Delta HDF\) và \(\Delta HEI\) ta có
\(BC\perp DF;BC\perp EI\) => BC đi qua trung điểm của DF và EI => tg HDF và tg HEI là tam giác cân tại H (có BC là đường cao đồng thời là đường trung trực)
\(\Rightarrow\widehat{HEI}=\widehat{HIE};\widehat{HDF}=\widehat{HFD}\) (góc ở đáy của tg cân)
Ta có DF//EI (cùng vuông góc với BC) => sđ cung DE = sđ cung FI (Trong đường tròn hai cung bị chắn bởi 2 dây // với nhau thì = nhau)
\(\Rightarrow\widehat{HFD}=\widehat{HEI}\) (góc nội tiếp cùng chắn 2 cung có số đo bằng nhau)
\(\Rightarrow\widehat{HEI}=\widehat{HIE}=\widehat{HDF}=\widehat{HFD}\) => tg HDF đồng dạng với tg HEI
\(\Rightarrow\frac{HD}{HE}=\frac{HF}{HI}\Rightarrow HD.HI=HE.HF\)

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

a) Xét tứ giác BFEC: ^BFC=^BEC=900 => Tứ giác BFEC là tứ giác nội tiếp đường tròn (đpcm).
b) Dễ thấy tứ giác ABKC nội tiếp đường tròn (O) => ^CAK=^CBK hay ^CAN=^CBK (1)
AK là đường kính của (O); B nằm trên (O) => AB\(\perp\)BK
Mà CF\(\perp\)AB => BK//CF => ^CBK=^BCF (2)
(1); (2) => ^CAN=^BCF. Mà ^BCF=^CAH (Cùng phụ ^ABC) => ^CAN=^BAH hay ^CAN=^FAM
Lại có: ^ACN=^AHE (Cùng phụ ^HAC)
Dễ chứng minh tứ giác AFHE nội tiếp đường tròn => ^AHE=^AFE
=> ^ACN=^AFE. Hay ^ACN=^AFM
Xét \(\Delta\)AMF và \(\Delta\)ANC: ^ACN=^AFM; ^CAN=^FAM => \(\Delta\)AMF ~ \(\Delta\)ANC (g.g)
=> \(\frac{AM}{AN}=\frac{MF}{NC}\)(*)
=> ^AMF=^ANC => 1800 - ^AMF=1800 - ^ANC => ^FMH=^CNK
Tứ giác ABKC nội tiếp (O) => ^ABC=^AKC. Mà ^ABC=^AHF (Cùng phụ ^BAH)
=> ^AKC=^AHF hay ^NKC=^MHF.
Xét \(\Delta\)NCK và \(\Delta\)MFH: ^NKC=^MHF; ^CNK=^FMH => \(\Delta\)NKC ~ \(\Delta\)MFH (g.g)
=> \(\frac{HM}{NK}=\frac{FM}{NC}\)(**)
Từ (*) và (**) => \(\frac{AM}{AN}=\frac{HM}{NK}\Rightarrow\frac{AM}{HM}=\frac{AN}{NK}\)=> MN//HK (Định lí Thales đảo) (đpcm).