Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c:
Xét tứ giác APMQ có
\(\widehat{APM}=\widehat{AQM}=\widehat{PAQ}=90^0\)
Do đó: APMQ là hình chữ nhật
Suy ra: PQ=AM

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
hay ΔABC vuông tại A

Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)

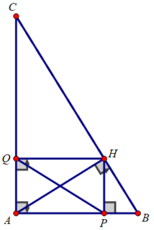
b)Xét tam giác ABC vuông tại A có:
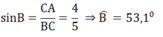
∠B + ∠C = 90 0 ⇒ ∠C = 90 0 - 53 , 1 0 = 36 , 9 0
Xét tứ giác APHQ có:
∠(PAQ) = ∠(AQH) = ∠(APH) = 90 0
⇒ Tứ giác APHQ là hình chữ nhật
⇒ PQ = AH = 12/5 (cm)

muốn giúp lắm nhưng mới lớp 7 chỉ bt làm phần a,d nghĩ bài a,d là toán lớp 7
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A