Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Ta có
BK=KC (GT)
AK=KD( Đối xứng)
suy ra tứ giác ABDC là hình bình hành (1)
mà góc A = 90 độ (2)
từ 1 và 2 suy ra tứ giác ABDC là hình chữ nhật
b) ta có
BI=IA
EI=IK
suy ra tứ giác AKBE là hình bình hành (1)
ta lại có
BC=AD ( tứ giác ABDC là hình chữ nhật)
mà BK=KC
AK=KD
suy ra BK=AK (2)
Từ 1 và 2 suy ra tứ giác AKBE là hình thoi
c) ta có
BI=IA
BK=KC
suy ra IK là đường trung bình
suy ra IK//AC
IK=1/2AC
mà IK=1/2EK
Suy ra EK//AC
EK=AC
Suy ra tứ giác AKBE là hình bình hành

a: Xét tứ giác AEIF có
\(\widehat{AEI}=\widehat{AFI}=\widehat{FAE}=90^0\)
Do đó: AEIF là hình chữ nhật

1a/IM vuông góc AB=>AMI=90 do
IN vuông góc AC=>ANI=90 do
△ABC vuông tại A=>BAC=90 do
=>góc AMI= gocANI= gocBAC= 90 do => tứ giác AMIN là hình chữ nhật
1b/Có I dx vs D qua N => ID là đường trung trực của AC=>AI=AD; IC=ID(1)
Trong △ABC có AI là đường trung tuyến ứng với cạnh huyền BC =>AI=1/2BC hay AI=IC(2)
Từ (1) va (2) => AI=IC=CD=DA => Tu giac AICD la hthoi
2a/ Có M là TĐ AB và M là điểm đối xứng giữa E và H
=> AM=MB VA EM=MH hay AB giao voi EH tai TD M
=> Tg AEBH la hbh co AHB=90 do => Hbh AEBH la hcn
2b/Co AEBH la hcn=>EH=AB
+) Mà AB=AC=>EH=AC(1)
+) △ABC cân tại A có AH là đường cao đồng thời phân giác của góc BAC => góc BAH=góc HAC.
Co goc BAH=1/2 EAH ; góc AHE=1/2AHB
Ma goc EAH= goc AHB=>BAH=AHE hay goc HAC= goc AHE.
Mà 2 góc này ở vị trí SLT=> EH//AC(2)
Từ (1) va (2)=>tg AEHC la hbh

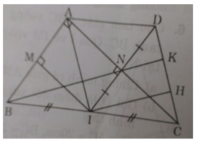
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.

a,Xét tứ giác ABDC có:
D đối xứng với A qua M nên :
DA=DC(1)
M là trung điểm BC nên:
BM=MC(2)
Từ (1)và (2) suy ra:
tứ giác ABDC là hình chữ nhật(đpcm)
b, vì ABDC là hình chữ nhật nên:
AB=DC và AB//DC
mà DC=FC và F trên tia DC
=>AB=FC và AB//FC
vậy tứ giác ABCF là hình bình hành(đpcm)

a: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật
