Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: CD=AB(1)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(CD^2=BH\cdot BC\)

1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )

a) Ta có: Đường tròn (O) đường kính BC và 2 điểm D;E nằm trên (O)
=> ^BEC=^BDC=900 => BD vuông AC; CE vuông AB
Mà BD gặp CE tại H => H là trực tâm \(\Delta\)ABC
=> AH vuông BC (tại F) hay AF vuông BC (đpcm).
b) Thấy: \(\Delta\)ADH vuông đỉnh D, M là trg điểm AH
=> \(\Delta\)DMA cân đỉnh M => ^MDA=^MAD (1).
Tương tự: \(\Delta\)DOC cân đỉnh O => ^ODC=^OCD (2).
(1) + (2) => ^MAD+^ODC = ^MDA+^ODC = ^MAD+^OCD
Mà 2 góc ^MAD; ^OCD phụ nhau (Do \(\Delta\)AFC vuông đỉnh F)
=> ^MDA+^ODC=900 => ^MDO=900 => MD vuông OD
Lập luận tương tự: ME vuông OE => Tứ giác MEOD có ^MEO=^MDO=900
=> MEOD là tứ giác nội tiếp đường tròn đường kính OM
Xét tứ giác MFOD: ^MFO=^MDO=900 => Tứ giác MFOD nội tiếp đường tròn đường kính MO.
Do đó: 5 điểm M;D;O;E;F cùng thuộc 1 đường tròn đường kính OM (đpcm).
c) Dễ c/m \(\Delta\)EBF ~ \(\Delta\)CDF (c.g.c) => ^EFB=^CFD
=> 900 - ^EFB = 900 - ^CFD => ^EFA=^DFA hay ^EFM=^MFD
Xét tứ giác FEMD: Nội tiếp đường tròn => ^EFM=^KDM => ^MFD=^KDM
=> \(\Delta\)MKD ~ \(\Delta\)MDF (g.g) => \(\frac{MD}{MF}=\frac{MK}{MD}\Rightarrow MD^2=MK.MF\)(đpcm).
Gọi I là giao điểm BK và MC.
Dễ thấy: \(\Delta\)FEK ~ FMD (g.g) => \(\frac{FE}{FM}=\frac{FK}{FD}\Rightarrow FE.FD=FM.FK\)
Hoàn toàn c/m được: \(\Delta\)EFB ~ \(\Delta\)CFD (c.g.c) => \(\frac{FE}{FC}=\frac{BF}{FD}\Rightarrow FE.FD=BF.FC\)
Từ đó suy ra: \(FM.FK=BF.FC\)\(\Rightarrow\frac{BF}{FM}=\frac{FK}{FC}\)
\(\Rightarrow\Delta\)BFK ~ \(\Delta\)MFC (c.g.c) => ^FBK=^FMC . Mà ^FMC+^FCM=900
=> ^FBK+^FCM = 900 hay ^FBI+^FCI=900 => \(\Delta\)BIC vuông đỉnh I
=> BK vuông với MC tại điểm I.
Xét \(\Delta\)MBC: BK vuông MC (cmt); MK vuông BC (tại F) => K là trực tâm \(\Delta\)MBC (đpcm).
d) Thấy ngay: EH là phân giác trong của \(\Delta\)FEK. Mà EA vuông EH
=> EA là phân giác ngoài tại đỉnh E của \(\Delta\)FEK
Theo ĐL đường phân giác trg tam giác: \(\frac{KH}{FH}=\frac{AK}{AF}\)
\(\Leftrightarrow1+\frac{KH}{FH}=1+\frac{AK}{AF}\Rightarrow\frac{FK}{FH}=\frac{AK+AF}{AF}\Leftrightarrow\frac{FK}{FH}=\frac{FK+2AK}{AF}\)
\(\Leftrightarrow\frac{FK}{FH}=\frac{FK}{AF}+\frac{2AK}{AF}\Leftrightarrow\frac{FK}{AF}=\frac{FK}{FH}-\frac{2AK}{AF}\)
\(\Leftrightarrow\frac{FK}{AF}+\frac{FK}{FH}=\frac{2FK}{FH}-\frac{2AK}{AF}=2+\frac{2KH}{FH}-2+\frac{2KF}{AF}=\frac{2KH}{FH}+\frac{2KF}{AF}\)
\(\Rightarrow FK\left(\frac{1}{AF}+\frac{1}{FH}\right)=\frac{2KH}{FH}+\frac{2KF}{AF}\)
Đến đây, lại thay: \(\frac{KH}{FH}=\frac{AK}{AF}\)(T/c đg phân giác)
\(\Rightarrow FK\left(\frac{1}{AF}+\frac{1}{FH}\right)=\frac{2\left(AK+KF\right)}{AF}=\frac{2AF}{AF}=2\)
\(\Leftrightarrow\frac{1}{AF}+\frac{1}{FH}=\frac{2}{FK}.\)(đpcm).
d.
Xét△FBH và △FAC có BFH=AFC=90*,FBH=FAC(cùng phụ BCD)
=>△FBH∼ △FAC(g.g) =>FH.FA=FB.FC .
Xét△FBK và △FMC có BFK=MFC=90*, FBK=FMC
=>△FBK ∼ △FMC(g.g)=>FK.FM=FB.FC .
=>FH.FA=FK.FM
Mà FH+FA=FM-MH+FM+MA=2FM
Ta có 2FH.FA=2FK.FM=>2FH.FA=FK(FH+FA)=>KL

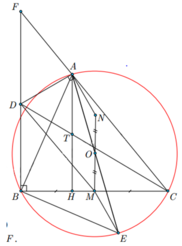
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
a/
Xét tg ABC có
\(AB^2=BH.BC\) (trong tg vuông bình phương cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\)
\(\sin\widehat{ACB}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
b/ Ta có
MB=MC (gt); MA=MD (gt) =>ABDC là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> AB=CD (cạnh đối hbh) mà \(AB^2=BH.BC\) (cmt)
\(\Rightarrow CD^2=BH.BC\)
c/ Ta có
ABDC là hình bình hành (cmt)
\(A=90^o\) (gt)
=> ABDC là hình chữ nhật \(\Rightarrow BD\perp CQ\) (1)
\(AH\perp BC\) (gt) \(\Rightarrow QH\perp BC\) (2)
Từ (1) và (2) => T là trực tâm của tg BCQ