

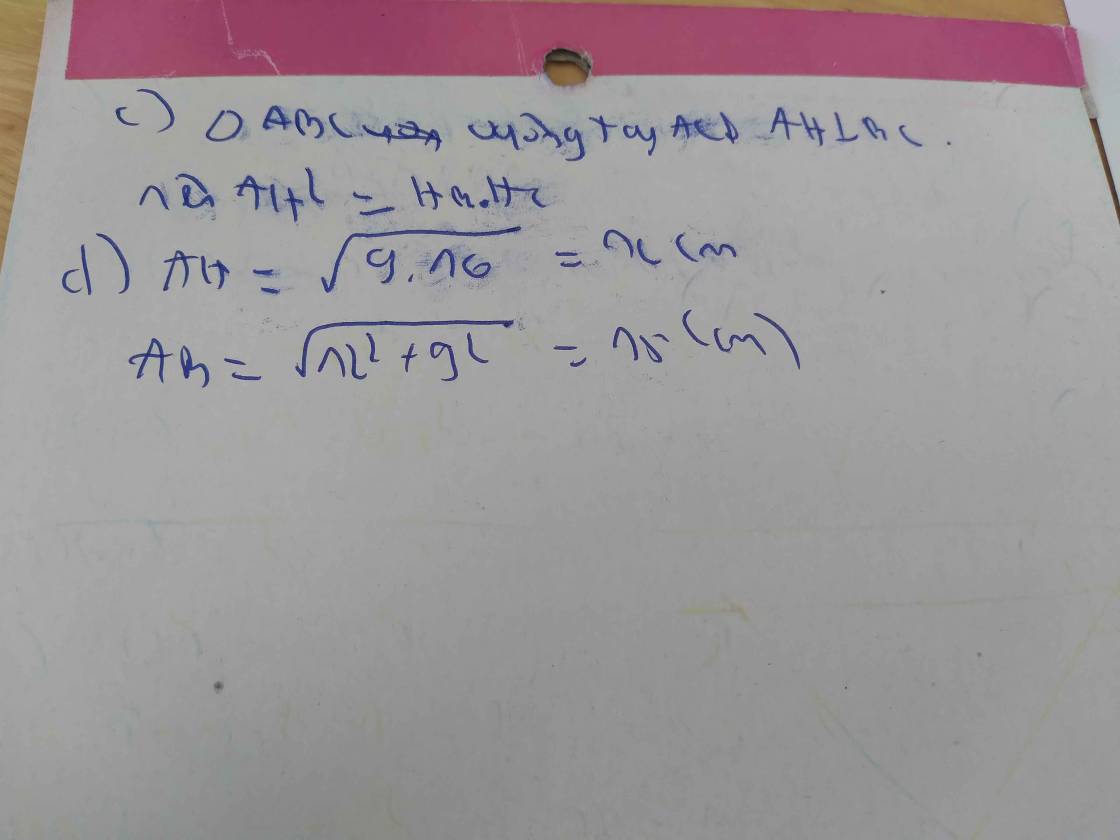
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



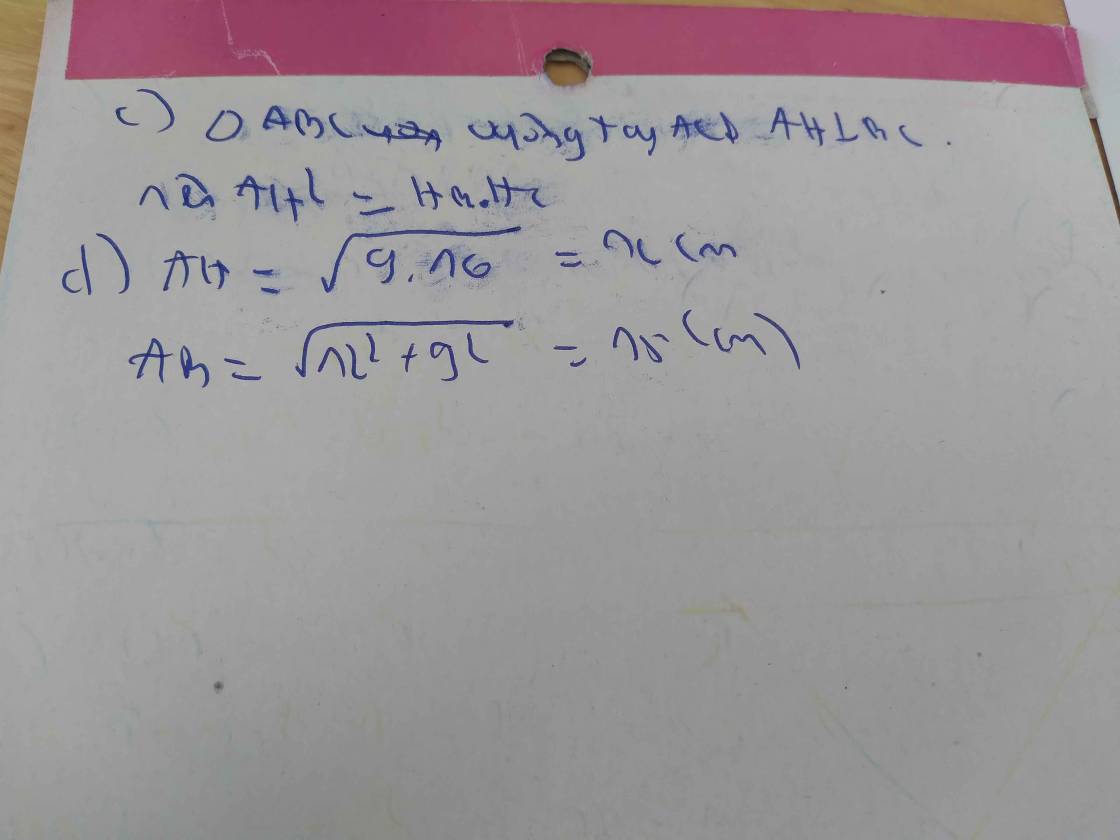

Xét tứ giác ABKC có:
\(B\chi\perp AB\) (gt)
\(AC\perp AB\) (gt)
\(\Rightarrow B\chi\text{//}AC\)
\(\Rightarrow\text{Tứ giác ABKC}\) là hình thang
mà \(\widehat{A}=\widehat{B}=\)\(90^0\)
Vậy hình thang ABKC là hình thang vuông
b) Xét ΔABK và ΔCHA có:
\(\widehat{ABK}=\widehat{CHA}=\)\(90^0\)
\(\widehat{BAK}=\widehat{HCA} \) ( cùng phụ với \(\widehat{HAC}\) )
\(\Rightarrow\text{ΔABK}\) \(\sim\)ΔCHA (gg)
\(\Rightarrow\dfrac{AB}{CH}=\dfrac{AK}{CA}\)
\(\Rightarrow AB.CA=AK.CH\)
c) Xét ΔAHB và ΔCHA có:
\(\widehat{AHB}=\widehat{CHA}=\)\(90^0\)
\(\widehat{BAH}=\widehat{HCA}\) ( cùng phụ với \(\widehat{HAC}\) )
\(\Rightarrow\Delta AHB\sim\Delta CHA\left(gg\right)\)
\(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\)
\(\Rightarrow AH.AH=BH.CH\)
\(\Rightarrow AH^2=BH.CH\)
\(\Rightarrow AH^2=9.16\)
\(\Rightarrow AH=12\left(cm\right)\)
Xét \(\Delta AHB\) vuông tại H có:
\(AB^2=BH^2+HA^2\) ( Định lí Pitago)
\(\Rightarrow AB^2=9^2+12^2\)
\(\Rightarrow AB=\sqrt{225=15\left(cm\right)}\)

a) Xét Tứ giác ABKC có:
Bx vuông AB (gt)
AC vuông AB (gt)
=> Bx //AC.
=> Tứ giác ABKC là hình thang.
mà góc A= Góc B =90 đô.
Vậy hình thang ABKC là hình thang vuông.
b) Xét \(\Delta ABK\)vuông và \(\Delta CHA\)vuông :
Góc B = Góc H = 90 độ (gt)
Góc BAK = góc HCA ( cùng phụ góc HAC)
\(\Rightarrow\Delta ABK\infty\Delta CHA\)
c) Xét \(\Delta AHB\)vuông và \(\Delta CHA\)vuông:
Góc BHA = Góc AHC = 90 độ (gt)
Góc BAH = góc HCA (cùng phụ HAC)
\(\Rightarrow AHB\infty CHA\)
\(\Rightarrow\frac{AH}{CH}=\frac{HB}{AH}\Rightarrow AH^2=HC.HB\)
đề sai á: nếu HB.AC thì cac goc trong tam giác này ko đồng dạng.

a: Xét tứ giác ABKC có BK//AC
nên ABKC là hình thang
mà góc CAB=90 độ
nên ABKC là hình thang vuông
b: Xét ΔaBK vuông tại B và ΔCHA vuông tại H có
góc BAK=góc HCA
Do đó ΔABK\(\sim\)ΔCHA
Suy ra: AB/CH=AK/AC
hay \(AB\cdot AC=AK\cdot CH\)
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
d: \(BC=BH+CH=25\left(cm\right)\)
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)

a) tứ giác ABKC là hình thang vuông.
có AC vuông góc với AB, BK vuông góc góc AB
=> AC song song với BK (từ vuông góc đến song song)
=> tứ giác ACKB là hình thang và có góc CAB =900 (gt)
=> tứ giác ACKB là hình thang vuông
b) Theo câu a) ACKB là hình thang => AC song song với KB
=> góc CAK = góc AKB (so le trong)
Xét tam giác ABK và tam giác CHA có:
góc CAK = góc AKB (CM/trên)
và góc ABK = góc CHA (=900)
=> tam giác ABK đồng dạng với tam giác CHA (g-g)
\(\Rightarrow\dfrac{AB}{CH}=\dfrac{AK}{AC}\Rightarrow AB.AC=AK.CH\)
c) Xét tam giác CAH thì có góc CAH = 900 - góc ACH (1)
Xét tam giác ABC thì góc ABC = 900 - góc ACH (2)
Từ (1)(2)=. góc CAH = góc ABC
Xét tam giác CAH và tam giác ABH có:
góc CAH = góc HBA (CM/trên)
và góc CHA = góc AHB (=900)
=> tam giác CAH đồng dạng với tam giác ABH (g-g)
=> \(\dfrac{AH}{BH}=\dfrac{CH}{AH}\Rightarrow AH^2=CH.BH\)
d) Theo câu c) ta có \(AH^2=BH.CH\) thay số vào ta được:
\(AH^2=9.16=144\Rightarrow AH=12\left(cm\right)\)
Áp dụng định lí Py-ta-go vào tam giác AHB ta có:
\(AB^2=AH^2+HB^2=12^2+9^2=225\Rightarrow AB=15\left(cm\right)\)
hôm nào tớ thấy bn cũng có bài tập toàn bài tập dễ mà ko chịu làm ![]()

a: Xét tứ giác ABKC có
AC//BK
góc BAC=90 độ
=>ABKC là hình thang vuông
b:
AH=AB*sin60=a*căn 3/2
BH=a/2
Xét ΔHAC vuông tại A và ΔHKB vuông tại H có
góc HAC=góc HKB
=>ΔHAC đồng dạng vớiΔHKB
=>HA/HK=HC/HB
=>HK*HC=HA*HB=a*căn 3/2*a/2=a^2*căn 3/4

a, Xét tứ giác ABKC có: AC // BK ( cùng vuông góc vs AB)
=> Tứ giác ABKC là hình thang
mà \(\widehat{A}=90^o\)=> Tứ giác ABKC là hình thang vuông
b) Ta có: AC // BK => \(\widehat{AKB}=\widehat{CAH}\)( 2 góc so le trong)
Xét tam giác ABK và tam giác CHA có:
\(\widehat{ABK}=\widehat{CHA}\left(=90^o\right)\)
\(\widehat{AKB}=\widehat{CAH}\)(cmt)
=> Tam giác ABK đồng dạng với tam giác CHA
=> \(\frac{AB}{AK}=\frac{CH}{AC}\)=> AB. AC = AK.CH (đpcm)
c) Xét tam giác ABH và tam giác CAH có:
\(\widehat{AHB}=\widehat{CHA}\left(=90^o\right)\)
\(\widehat{BAH}=\widehat{ACH}\)( cùng phụ với góc HAC)
=> Tam giác ABH đồng dạng với tam giác CAH
=> \(\frac{AH}{BH}=\frac{CH}{AH}\)=> \(AH^2=BH.CH\)
d) Ta có: \(AH^2=BH.CH\)(cmc) => \(AH=\sqrt{BH.CH}=\sqrt{9.16}=12\)(cm)
Xét tam giác ABH vuông tại H, ta có: \(AB^2=BH^2+AH^2\)(định lý Pytago)
=> \(AB=\sqrt{BH^2+AH^2}=\sqrt{9^2+12^2}=15\)(cm)
Vậy AB = 15cm, AH = 12cm
Chúc bạn học tốt

â ) Ta có : AC \(\perp\) AB ( tam giác ABC vuông tại A )
: BK \(\perp\)AB ( gt )
Do đo : AC // BK ( vì cùng vuông góc với AB )
Xét tứ giác ABKC , ta có :
\(\widehat{A}=90^O\) ( tam giác ABC vuông tại A )
\(\widehat{B}=90^O\left(gt\right)\)
AC // BK ( cmt )
Do đo : tứ giác ABKC là hình thang vuông
b ) Ta co : AC // BK ( cmt )
=> \(\widehat{K_1}=\widehat{A_2}\) ( hai góc so le trong của hai đường thẳng song song )
Xét :\(\Delta BAKva\Delta HCA,taco:\)
\(\widehat{B}=\widehat{H}=90^o\)
\(\widehat{K_1}=\widehat{A_2}\left(cmt\right)\)
Do do : \(\Delta BAK\) đồng dạng \(\Delta HCA\)( g - g )
= > \(\frac{AB}{AK}=\frac{CH}{AC}\)
=> AC . AC = AK . CH
c) CÂU NÀY CÓ 2 CÁCH NHA
Cach 1 )
Ta có : \(\widehat{A_1}+\widehat{B_1}=90^o\) ( tổng số đo hai góc nhọn trong tam giác vuông )
mà : \(\widehat{A_1}+\widehat{A_2}=90^o\) ( tia AK nằm giữa hai tia AB và AC )
nên \(\widehat{B_1}=\widehat{A_2}\) ( cung phụ vào góc \(\widehat{A_1}\) )
Xét : \(\Delta ABHva\Delta CAH,taco:\)
\(\widehat{H_1}=\widehat{H_2}=90^o\)
\(\widehat{B_1}=\widehat{A_2}=\left(cmt\right)\)
Do do : \(\Delta ABH\) đồng dạng \(\Delta CAH\left(g-g\right)\)
\(=>\frac{HC}{AH}=\frac{AH}{HB}\)
\(=>AH.AH=HB.HC\)
\(AH^2=9.16\)
\(AH^2=144\)
\(AH=\sqrt{144}=12cm\)
Áp dụng định lý pytago vào \(\Delta ABH\) vuông tại H
\(AB^2=AH^2+BH^2\)
\(AB=\sqrt{12^2+9^2}\)
\(AB=\sqrt{144+81}\)
\(AB=\sqrt{225}\)
\(AB=15cm\)
Cách 2 : ( của lớp 9 nha )
Ta có : BC = BH + HC = 9 + 16 = 25cm ( vì H nằm giữa B và C )
Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại A ( \(\widehat{A}=90^o;AH\perp BC\) )
\(AB^2=BH.BC\)
\(AB^2=9.25\)
\(AB^2=225\)
\(AB=\sqrt{225}=15cm\)
Áp dụng định lý pytago vào \(\Delta ABH\) vuông tại H
\(AH^2=AB^2-BH^2\)
\(AH^2=15^2-9^2\)
\(AH^2=225-81\)
\(AH^2=144\)
\(AH=\sqrt{144}=12cm\)
CÒN NHIỀU CÁCH NỮA NHA
OK CHÚC BẠN HỌC TỐT !!!!!
a) Ta có : \(KB\perp AB\)
\(AC\perp AB\)
\(\Rightarrow BK//AC\)
\(\Rightarrow\) tứ giác ABKC là hình thang
b) Ta có BK // AC
\(\Rightarrow\widehat{AKB}=\widehat{KAC}\)( so le trong )
Xét tam giác BAK và tam giác HCA có :
\(\widehat{AKB}=\widehat{KAC}\)
\(\widehat{ABK}=\widehat{AHC}\left(=90^o\right)\)
\(\Rightarrow\)tam giác BAK đồng dạng với tam giác HCA ( g-g ) (đpcm)
\(\Rightarrow\frac{BA}{HC}=\frac{AK}{CA}\)
\(\Leftrightarrow AB\times AC=AK\times CH\left(đpcm\right)\)
c) Xét tam giác ABC và tam giác HBA có :
\(\widehat{BAC}=\widehat{AHB}\left(=90^o\right)\)
Chung \(\widehat{ABC}\)
\(\Rightarrow\) tam giác ABC đồng dạng với tam giác HBA ( g-g )
\(\Rightarrow\frac{AB}{HB}=\frac{BC}{AB}\)
\(\Leftrightarrow AB^2=BC\times HB\)
\(\Leftrightarrow AB^2=\left(9+16\right)\times9\)
\(\Leftrightarrow AB^2=225\)
\(\Leftrightarrow AB=15\left(cm\right)\)
Áp dụng định lý Pi-ta-go cho tam giác ABH vuông tại H ta có :
\(BH^2+AH^2=AB^2\)
\(\Leftrightarrow9^2+AH^2=15^2\)
\(\Leftrightarrow81+AH^2=225\)
\(\Leftrightarrow AH=12\left(cm\right)\)
Vậy AB = 15 cm ; AH = 12 cm

a: Xét ΔAHB vuông tại H và ΔCHA vuôg tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
MH/MC=AH/AC=HB/AB
b: Xét ΔABE và ΔCMA có
góc BAE=góc MCA
góc ABE=góc CMA
=>ΔABE đồng dạng vơi ΔCMA
=>góc AEB=góc CAM
=>góc BEA=góc EAM
=>AM//BE