V
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
10 tháng 5 2018
Áp dụng tỉ số tanB trong tam giác vuông HAB và các hệ thức lượng trong tam giác vuông, chúng ta tính được AC = 30 13 cm; BM = 601 4 cm
PN
26 tháng 12 2016
\(tan\text{ }B\text{ }-3.tan\text{ }C=tan\text{ }60^o-3.tan\text{ }30^o=\sqrt{3}-3.\frac{1}{\sqrt{3}}=0\text{ }\text{ }\text{ }\text{ }\text{ }\)
3 tháng 9 2021
a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan30^0\)
\(=2\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2021
\(tanB=\sqrt{2}\Rightarrow\dfrac{AC}{AB}=\sqrt{2}\Rightarrow\dfrac{AC^2}{AB^2}=2\)
\(\Rightarrow\dfrac{AC^2}{AB^2}+1=3\Rightarrow\dfrac{AC^2+AB^2}{AB^2}=3\Rightarrow\dfrac{BC^2}{AB^2}=3\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{1}{\sqrt{3}}\)
Mà \(sinC=\dfrac{AB}{BC}\Rightarrow sinC=\dfrac{1}{\sqrt{3}}\)
\(sin^2C+cos^2C=1\Rightarrow\dfrac{1}{3}+cos^2C=1\Rightarrow cosC=\dfrac{\sqrt{6}}{3}\)
\(tanC=\dfrac{sinC}{cosC}=\dfrac{\sqrt{2}}{2}\)
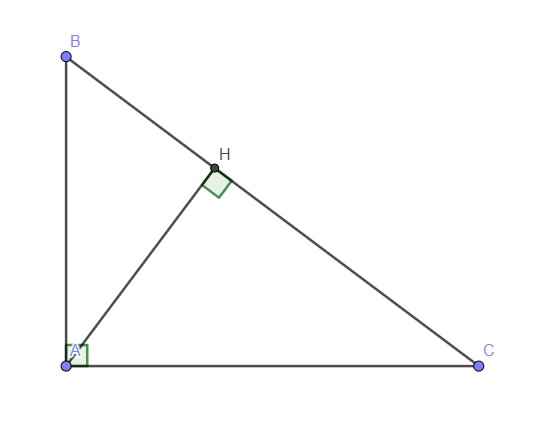
b.
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{sinC}=\dfrac{2\sqrt{3}}{\dfrac{1}{\sqrt{3}}}=6\left(cm\right)\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AB=\dfrac{AC}{tanB}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)
Áp dụng Pitago:
\(BC=\sqrt{AB^2+AC^2}=3\sqrt{6}\left(cm\right)\)
\(tanB=tan15^0=2-\sqrt{3}\)
Cách tính cụ thể:
Trên tia AC lấy D sao cho \(\widehat{ABD}=30^0\Rightarrow BC\) là phân giác của \(\widehat{ABD}\)
Theo định lý phân giác: \(\dfrac{AC}{AB}=\dfrac{CD}{BD}=\dfrac{AC+CD}{AB+BD}=\dfrac{AD}{AB+BD}\) (1)
Lại có: \(tan\widehat{ABD}=tan30^0=\dfrac{AD}{AB}=\dfrac{1}{\sqrt{3}}\Rightarrow AB=\sqrt{3}AD\) (2)
\(sin\widehat{ABD}=sin30^0=\dfrac{AD}{BD}=\dfrac{1}{2}\Rightarrow BD=2AD\) (3)
Thế (2); (3) vào (1):
\(\dfrac{AC}{AB}=\dfrac{AD}{\sqrt{3}AD+2AD}=2-\sqrt{3}\)
\(\Rightarrow tanB=\dfrac{AC}{AB}=2-\sqrt{3}\)