Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\left(pytago\right)\)
\(b,\) Vì \(\widehat{BAC}=\widehat{AHB}\left(=90\right);\widehat{ABC}.chung\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)
\(c,\Delta ABC\sim\Delta HBA\left(cm.trên\right)\\ \Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\Rightarrow AB^2=BH\cdot BC\)
\(d,\) Vì AD là p/g góc A
\(\Rightarrow\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\\ \Rightarrow DC=\dfrac{4}{3}BD\)
Mà \(BD+DC=BC=10\)
\(\Rightarrow\dfrac{4}{3}BD+BD=10\\ \Rightarrow\dfrac{7}{3}BD=10\\ \Rightarrow BD=\dfrac{30}{7}\left(cm\right)\)

a. áp dụng định lý py-ta-go vào tam giác ABC, ta có:
AB2+AC2=BC2
62+82= BC2
36+64= BC2
BC2=100
BC= 10 (cm)
b. bạn thiếu đề rồi ạ.

a) Xét ΔHBA và ΔABC có
\(\widehat{B }\) chung
\(\widehat{BHA}=\widehat{BAC}\)=90o
=> ΔHBA ∼ ΔABC (gg)
b) xét ΔABC có \(\widehat{BAC} \)=90o
=> AC2+AB2=BC2 (đl pitago)
=>162+122=BC2
=> BC=20 cm
Ta có SΔABC=\(\dfrac{AB.AC}{2}=\dfrac{AH.BC}{2}\)
=> AB.AC=AH.BC
=>12.16=AH.20
=> AH=9.6
Xét ΔABH có \(\widehat{BHA}\)=90o
=> HA2+HB2=AB2 (đl pitago)
=>9.62 + HB2=122
=> HB=7.2 cm
c) Xét ΔABC có
AD là phân giác (D∈BC)
=> \(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{12}{16}=\dfrac{3}{4}\)(tc đường pg trong Δ)
=>\(\dfrac{BD}{BC-BD}=\dfrac{3}{4}\)=>\(\dfrac{BD}{20-BD}=\dfrac{3}{4}\)
=> BD=\(\dfrac{60}{7}\) cm
=> CD=20 - \(\dfrac{60}{7}\)=\(\dfrac{80}{7}\) cm
d) Xét ΔAHC có
KN // HC (MN//BC , K ∈ MN , H∈ BC,(K∈AH ,N∈AC))
=> \(\dfrac{AN}{AC}=\dfrac{AK}{AH}=\dfrac{KN}{HC}\)( hệ quả đl ta-lét)
=>\(\dfrac{AN}{AC}=\dfrac{3.6}{9.6}=\dfrac{KN}{HC}\)
Xét ΔABC có
MN// BC (M∈AB ,N∈AC)
=> \(\dfrac{AN}{AC}=\dfrac{MN}{BC}\)=>\(\dfrac{3.6}{9.6}=\dfrac{MN}{20}\) => MN =7.5 cm
KH=AH-KH =9.6-3.6=6 cm
Xét tg MNCB có MN//BC
=> tg MNCB là hình bình hành (dhnb)
có AH⊥BC => KH⊥BC (K∈AH)
=> SBMNC = \(\dfrac{KH.\left(MN+BC\right)}{2}\)=\(\dfrac{6.\left(7.5+20\right)}{2}\)=82.5cm2

Tự vẽ hình nha
a) xét tam giác HAB và tam giác ABC
góc AHB = góc ABC
góc CAB : chung
Suy ra : tam giác AHB ~ tam giác ABC ( g-g )
b) Áp dụng định lí py - ta - go vào tam giác ABC ta được :
AC2 + AB2 = BC2
162 + 122 = BC2
400 = BC2
=> BC = \(\sqrt{400}\)= 20 ( cm )
ta có tam giác HAB ~ tam giác ABC ( câu a )
=> \(\frac{AH}{AC}=\frac{AB}{BC}hay\frac{AH}{16}=\frac{12}{20}\)
=> AH = \(\frac{12.16}{20}=9,6\)( cm )
Độ dài cạnh BH là
Áp dụng định lí py - ta - go vào tam giác HBA ta được :
AH2 + BH2 = AB2
BH2 = AB2 - AH2
BH2 = 122 - 9,62
BH2 = 51,84
=> BH = \(\sqrt{51,84}\) = 7,2 ( cm )
c) Vì AD là đường phân giác của tam giác ABC nên :
\(\frac{AB}{BD}=\frac{AC}{CD}\Leftrightarrow\frac{AB}{BC-CD}=\frac{AC}{CD}\)
<=> \(\frac{AB.CD}{CD\left(BC-CD\right)}=\frac{AC\left(BC-CD\right)}{CD\left(BC-CD\right)}\)
<=> AB.CD = AC(BC - CD)
hay 12CD = 16.20 - 16CD
<=> 12CD+ 16CD = 320
<=> 28CD = 320
<=> CD = \(\frac{320}{28}\approx11.43\left(cm\right)\)
Độ dài cạnh BD là :
BD = BC - CD
BD = 20 - \(\frac{320}{28}\)\(\approx\) 8,57 ( cm )
Cho hỏi đồng dạng là sao bạn???Tớ mới học lớp 7 thôi,nên chưa biết ^^

a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
c: BA/BH=BC/BA
=>BA^2=BH*BC

xét Tam giác HBA và Tam giác ABC có
B Chung
Góc H=A(=90 độ)
=> tam giác HBA Đồng dạng với tam giác giác ABC (g.g)
=> AH/AC=AB/BC
(BC)^2=AB^2+AC^2
BC^2=400
BC=20
AH/AC=AB/BC => AH=AB.AC/BC=16x12/20=9.6

Tự vẽ hình nha
a) xét tam giác HAB và tam giác ABC
góc AHB = góc ABC
góc CAB : chung
Suy ra : tam giác AHB ~ tam giác ABC ( g-g )
b) Áp dụng định lí py - ta - go vào tam giác ABC ta được :
AC2 + AB2 = BC2
162 + 122 = BC2
400 = BC2
=> BC = = 20 ( cm )
ta có tam giác HAB ~ tam giác ABC ( câu a )
=>
=> AH = ( cm )
Độ dài cạnh BH là
Áp dụng định lí py - ta - go vào tam giác HBA ta được :
AH2 + BH2 = AB2
BH2 = AB2 - AH2
BH2 = 122 - 9,62
BH2 = 51,84
=> BH = = 7,2 ( cm )
c) Vì AD là đường phân giác của tam giác ABC nên :
<=>
<=> AB.CD = AC(BC - CD)
hay 12CD = 16.20 - 16CD
<=> 12CD+ 16CD = 320
<=> 28CD = 320
<=> CD =
Độ dài cạnh BD là :
BD = BC - CD
BD = 20 - 8,57 ( cm )
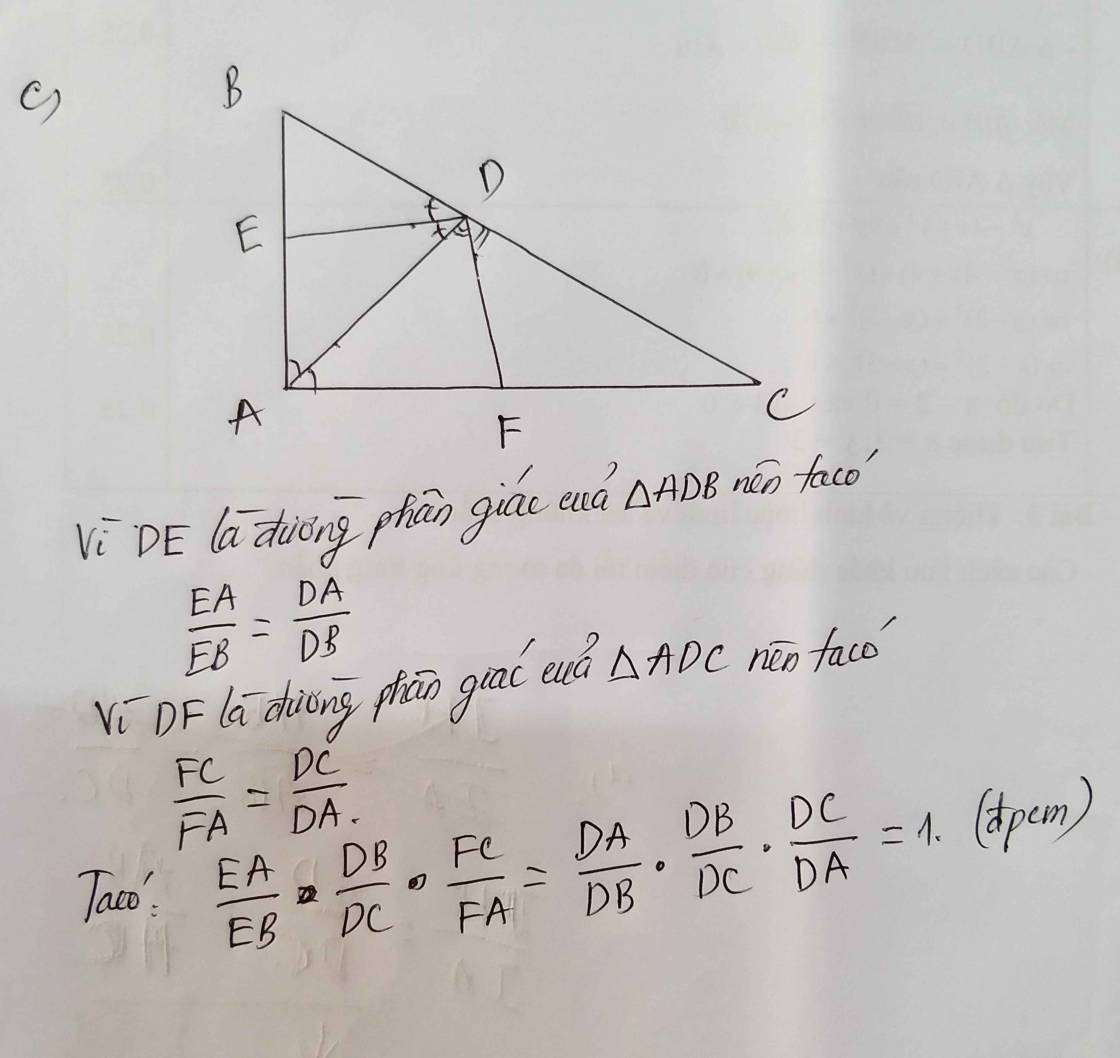
a: Xét ΔABC vuông tại A và ΔHBA vuôg tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*CB
c: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
BH=12^2/20=144/20=7,2cm
HC=20-7,2=12,8cm
d: AD là phân giác
=>DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=20/7
=>DB=60/7cm; DC=80/7cm
.