Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

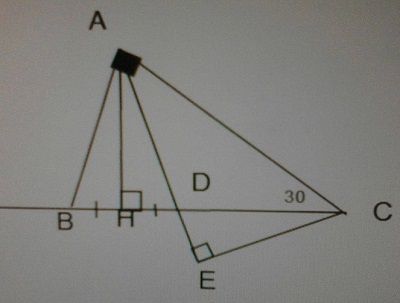
a) xét tam giác ABD có AH là đường cao( AH vuông góc với BC)
đồng thời AH là đường trung tuyến( HD=HB)
=> tam giác ABD cân tại A(1)
lại có tam gisc ABC vuông tại A, gocs C=30 độ
=> góc B=90 độ = 90-30 =60 độ(2)
từ(1) (2)=> tam giác ABD đều
b) tam giác ABD đều => góc BAD=60 độ
vậy ta có góc BAD+góc DAC=90
hay 60+góc DAC=90
góc DAC=30 độ
Xét tam giác ADC có góc DAC=góc DCA=30
Vậy tam giác ADC cân tại D=> AD=DC
Xét tam giác ADH và tam giác CDE có
góc DEC=góc DHA=90
AD=CD(cmt)
góc CDE=góc ADH(đối đỉnh)
=> tam giác ADH=tam giác CDE(ch-gc)
=> AH= CE(2 cạnh tương ứng)
a, xét tam giác ABD có AH là đường cao( AH vuông góc với BC)
đồng thời AH là đường trung tuyến( HD=HB)
=> tam giác ABD cân tại A(1)
lại có tam gisc ABC vuông tại A, godc C=30 độ
=> góc B=90 độ-gócc
=90-30 =60 độ(2)
từ(1) (2)=> tam giác ABD đều

(hình bạn tự kẻ nhé)
a) \(\Delta\)ABC : BAC^ = 90o ;BCA^ = 30o => ABC^ = 180o - BAC^ -BCA^ = 180o - 90o - 30o = 60o
\(\Delta\)BHA : BHA^ = 90o ; HBA^ = 60o => BAH^ = 180o - BHA^ - HBA^ = 180o - 90o - 60o = 30o
Xét \(\Delta\)BHA và \(\Delta\)DHA :
BHA^ = DHB^ = 90o
HA chung
HB = HD
=> \(\Delta\)BHA = \(\Delta\)DHA (2 cạnh góc vuông)
=> BAH^ = DAH^ = 30o (2 cạnh tương ứng)
Ta có: BAH^ + DAH^ = BAD^ <=> 30o + 30o = BAD^ => 60o = BAD^
\(\Delta\)ABD có: ABD^ = 60o; BAD^ = 60o
Và ABD^ + BAD^ + BDA^ = 180o
BDA^ = 180o - ABD^ - BAD^ = 180o - 60o - 60o = 60o
=> \(\Delta\)ABD đều
b) Ta có: \(\Delta\)BHA = \(\Delta\)DHA (cmt)
=> AH = CE (2 cạnh tương ứng)
c) Ta có: HDE^ = ADC^ (đđ)
và HDA^ = EDC^ = 60o (đđ)
mà HDE^ + ADC^ + HDA^ + EDC^ = 360o
2 * HDE^ + 2* HDA^ = 360o
2* HDE^ + 2* 60o = 360o
2* HDE^ = 360o - 120o
2* HDE^ = 240o
HDE^ = 120o
\(\Delta\)BHA = \(\Delta\)DHA (cmt)
=> DH = DE (2 cạnh tương ứng)
=> \(\Delta\)HDE cân tại D
=> DHE^ = DEH^
\(\Delta\)HDE có: DHE^ + DEH^ + HDE^ = 180o
2* DHE^ = 180o - HDE^ = 180o - 120o = 60o
DHE^ = 30o
=> DHE^ = DCA^ = 30o
Mà DHE^ sole trong với DCA^
=> EH // AC
a) ΔABDΔABD có đường cao AH đồng thời là đường trung tuyến nên ABDABD cân.
Có ˆB=600B^=600 (vì ˆC=300C^=300 (gt)).
Do đó ΔABDΔABD đều.
b) ΔABDΔABD đều (cmt) ⇒ˆBAD=600⇒ˆCAD=ˆC=300.⇒BAD^=600⇒CAD^=C^=300.
Do đó ΔADCΔADC cân tại D ⇒DA=DC.⇒DA=DC.
Xét hai tam giác vuông AHD và CED có:
+) DA=DCDA=DC (cmt);
+) ˆD1=ˆD2D^1=D^2 (đđ);
Vậy ΔAHD=ΔCEDΔAHD=ΔCED (cạnh huyền-góc nhọn)
⇒AH=CE.⇒AH=CE.
c) ΔAHD=ΔCEDΔAHD=ΔCED(cmt) ⇒HD=ED⇒HD=ED (cạnh tương ứng).
Do đó ΔDHEΔDHE cân tại D.
Mặt khác ΔADCΔADC cân tại D, mà hai tam giác cân này chung đỉnh D
⇒ˆCHE=ˆACB=300.⇒CHE^=ACB^=300.
⇒⇒ EH // AC (cặp góc so le trong bằng nhau).

a: Xét ΔAKC có
AH vừa là đường cao, vừa là trung tuyến
góc C=60 độ
=>ΔAKC đều
b: ΔKAB có góc KAB=góc KBA=30 độ
nên ΔKAB cân tạiK
=>KA=KB=KC
=>K là trung điểm của BC


a) Áp dụng tính chất tổng ba góc ta có :
A + B + C = 180 độ
90 độ + B + 30 độ = 180 độ
B = 60 độ
Xét tam giác AHB và tam giác ADH, có:
AH là góc chung
=> AHB = AHD = 90 độ
=> HB = HD (gt)
Vậy ADH = ABH (c.g.c)
=> AB = AD (có 2 cạnh tương ứng)
=> Tam giác ABD là tam giác đèu
b) ABD đều => BAD = 60 độ
Vậy BAD + DAC = 90 độ
=> 60 độ + DAC = 90 độ
=> DAC = 30 độ
Xét từng tam giác ta có :
Tam giác DAC có góc DAC = 30 độ
Vậy tam giác DAC cận tại D
=> AD = CD
Xét 2 tam giác ADH và CDE có DEC = DEH = 90 độ
=> AD = CD
=> CED = AHD
=> EHD = CED (ch - gc)
=> AH = CE
c) DE = DH (cạnh tương ứng)
Vậy DHE cân tại E.
=> DHE = (180 - EHD) : 2 => cân tại D
=> DAC = (180 - ADC) : 2 => ADC = EDH (đối đỉnh)
=> DEH = DAC
Mà DEH = DAC so le trong.
Vậy EH//AC

bạn tự vẽ hình nhé
a) ta có:
trong tam giác ABC:
 + góc B + góc C = 180
90 độ + góc B + 30 độ = 180 độ
=> góc B = 180 độ - 90 độ - 30 độ = 60 độ (1)
xét 2 tam giác vuông: ABH và ADH, có:
AH là cạnh chung
HD = HB (gt)
=> tam giác ABH = ADH (cạnh huyền - cạnh góc vuông)
=> AB = AD (2 cạnh tương ứng)
=>tam giác ABD cân tại A (2)
từ (1) , (2):
=> tam giác ABD đều (tam giác cân có 1 góc bằng 60 độ)
:D
Bn tự vẽ hình nhé!!!!
a)Xét tam giác AHB và tam giác AHD có:
AH là cạnh chung
\(\widehat{AHB}=\widehat{AHD}\left(=90^o\right)\)
HB=HD(GT)
Do đó:tam giác AHB=tam giác AHD(c-g-c)
\(\Rightarrow AB=AD\)(1)(2 cạnh tương ứng)
Từ D kẻ đg trung tuyến DK\(\Rightarrow\)DK là đg trung trực(TC về đg cao,trung tuyến,phân giác của tam giác cân)
Xét tam giác DAK và tam giác DBK có:
DK là cạnh chung
\(\widehat{DKA}=\widehat{DKB}\left(=90^o\right)\)
AK=BK(cách vẽ)
Do đó:tam giác DAK=tam giác DBK(c-g-c)
\(\Rightarrow\)DA=DB(2)(2 cạnh tương ứng)
Từ (1) và (2)\(\Rightarrow\)AB=AD=BD
Xét tam giác ABD có:AB=AD=BD(cmt)
Do đó:tam giác ABD là tam giác đều



a) Ta thấy :
Xét ∆ABM ta có :
AH là trung trực BM
=>∆ ABM cân tại A
Mà B = 60°
=> ∆ABM đều