Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
b:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC
c: Xét ΔADE có AH/AD=AK/AE
nên HK//DE
=>HK//BC

Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔACH
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH

+) Do tam giác ABC vuông cân tại A nên:
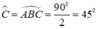
+) Tam giác ABD có AB = BD nên tam giác ABD cân tại B.
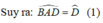
+) Tam giác ABD có góc ABC là góc ngoài tam giác tại đỉnh B nên:
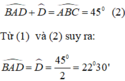

a: Xét ΔADB và ΔAEC có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔADB=ΔAEC
Suy ra: AD=AE
hay ΔADE cân tại A

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH

Ta có hình vẽ:
Ta có: tam giác ABC vuông cân tại A
=> góc ABC = 450
Ta có: góc ABC + góc ABD = 1800
hay 450 + góc ABD = 1800
=> góc ABD = 1800 - 450 = 1350
Ta có: góc DAB + góc ABD + góc ADB = 1800
hay góc DAB + góc ADB + 1350 = 1800
=> góc DAB + góc ADB = 450
Ta có: BD = BA => tam giác BDA cân
=> góc DAB = góc ADB = 450 /2 = 2205'
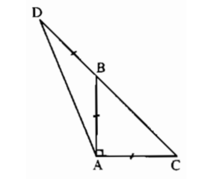
ΔABC vuông cân ở A (giả thiết) => ∠ABC = 45°.
ΔABD có BA = BD (giả thiết) => ΔABD cân ở B.
Mà ∠ABD, ∠ABC kề bù.
=> ∠ADB = (180° - ∠ABD)/2 = ∠ABC/2 = 45°/2 = 22,5°.