Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Phạm Ngọc Thạch - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

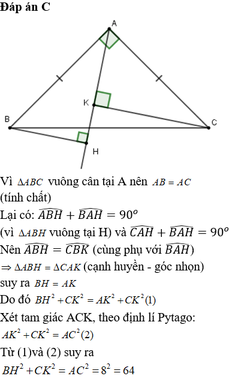
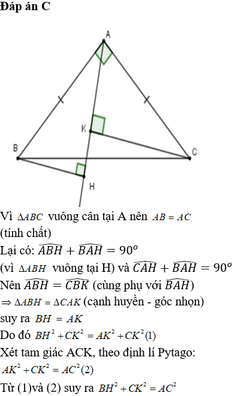
\(\widehat{ABH}=\widehat{CAK}\)(cùng phụ với \(\widehat{BAH}\))
Xét \(\Delta ABH\)và \(\Delta CAK\)có :
AH = AK(vì A là trung điểm của HK)
\(\widehat{A}_1=\widehat{A_2}\)(gt)
=> \(\Delta ABH=\Delta CAK\left(ch-gn\right)\)
=> BH = AK(hai cạnh tương ứng)
Do đó : \(BH^2+CK^2=AK^2+CK^2\) (1)
Xét \(\Delta\)vuông ACK,theo định lí Pi - ta - go :
\(AK^2+CK^2=AC^2\) (2)
Từ (1) - (2) suy ra : \(BH^2+CK^2=AC^2\)(hằng số)
Vậy \(BH^2+CK^2\)có giá trị không đổi

^HAB + ^BAC + ^KAC = 180
^BAC = 90
=> ^HAB + ^KAC = 90
xét tam giác ABH vuông tại H => ^BAH + ^ABH = 90
=> ^KAC = ^ABH
xét tam giác CKA và tam giác AHB có : AB = AC do tam giác ABC cân tại A (gt)
^CKA = ^AHB = 90
=> tam giác CKA = tam giác AHB (ch-gn)
=> CK = AH (đn)
xét tam giác ABH vuông tại H => BH^2 + AH^2 = AB^2 (Pytago)
=> BH^2 + CK^2 = AB^2
=> BH^2 + CK^2 không phụ thuộc vào d