Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

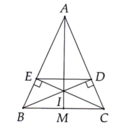
a) Xét ABD và EBD có
BD cạnh chung
BAD=BED(=90)
ABD=EBD(vì BD là tia phân giác của B)
b ko biet
b)Vì theo ý a) BAD=BED và BD là tia phân giác của B. Nên ADE là tam giác cân

a. Xét tam giác ABD và tam giác ACD
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
AD : cạnh chung
Vậy tam giác ABD = tam giác ACD ( c.g.c )
b. ta có trong tam giác ABC đường trung tuyến cũng là đường cao
=> AD vuông BC
CD = BC : 2 = 12 : 2 =6cm
c.áp dụng định lý pitago vào tam giác vuông ADC
\(AC^2=AD^2+DC^2\)
\(AD=\sqrt{10^2-6^2}=\sqrt{64}=8cm\)
d.Xét tam giác vuông BDE và tam giác vuông CDF có:
AD = CD ( gt )
góc B = góc C
Vậy tam giác vuông BDE = tam giác vuông CDF ( cạnh huyền . góc nhọn)
=> DE = DF ( 2 cạnh tương ứng )
=> tam giác DEF cân tại D
a) Tam giác ABD và tam giác ACD có:
BD = CD (Vì D là trung điểm của BC)
góc B = góc C
(vì tam giác ABC cân tại A)
AB = AC
Do đó: am giác ABD = tam giác ACD (c.g.c)
Suy ra: Góc ADB = góc ADC (cặp góc t/ứng)
b) Vì góc ADB = góc ADC (cmt) mà góc ADB + góc ADC 180 độ (2 góc kề bù)
nên góc ADB = 180 độ / 2 = 90 độ => AD vuông góc với BC
c) Ta có : BD + CD = BC ( Vì D nằm giữa B và C)
mà BC = 12 cm
=> CD = 12 /2 = 6 cm
Vì AD vuông góc với BC nên tam giác ADC vuông tại D
=> AC2AC2 = AD2AD2 +CD2CD2 (Định lý Pytago)
=> 10^2 = AD ^ 2 + 6 ^2
=> AD^2 = 64
=> AD = 8 (cm) (vì AD > 0 )
d) bạn c/m cho tam giác DEB = tam giác DFC (cạnh huyền - góc nhọn) nhé
=> DE = DF (cặp cạnh tương ứng) => tam giác DEF cân tại D( đn)

a)Xét \(\Delta ABD\) và \(\Delta ACD\) có :
\(BD=DC\)
\(\widehat{ABD}=\widehat{ACD}\left(\Delta ABCcân\right)\)
AB= AC
=> \(\Delta ABD\) = \(\Delta ACD\) (c-g-c)
b) Vì \(\Delta ABC\) cân tại A nên AD vừa là đường trung tuyến vừa là đường cao
=> \(AD\perp BC\)
*Nếu chx học cách trên thì bạn xem cách dưới đây"
Vì \(\Delta ABD\) = \(\Delta ACD\) nên \(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^o\)
=> \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^o}{2}=90^o\)
=> \(AD\perp BC\)
c)Xét \(\Delta EBD\) vuông tại E và \(\Delta FCD\) vuông tại F có :
\(\widehat{EBD}=\widehat{FCD}\)
\(BD=CD\)
=> \(\Delta EBD=\Delta FCD\left(ch-gn\right)\)
d) Vì D là trung điểm của BC nên \(DC=\dfrac{BC}{2}=\dfrac{12}{2}=6cm\)
Xét \(\Delta ADC\) vuông tại D có :
\(AC^2=AD^2+DC^2\)
\(100=AD^2+36\)
\(AD^2=100-36\)
\(AD^2=64\)
AD=8 cm

a, Ta có : AD = AB + BD ; AE = AC + CE
mà AB = AC (gt); BD = CE (gt)
=> AD = AE
Vậy tam giác ADE cân tại A
Ta có : \(\dfrac{AB}{AD}=\dfrac{AC}{AE}\)do AB = AC; AD = AE(cmt)
=> DE // BC ( Ta lét đảo )
b, Vì ^ABC = ^MDB ( đối đỉnh )
^ACB = ^NCE ( đối đỉnh )
mà ^ABC = ^ACB ( tam giác ABC cân tại A )
=> ^MDB = ^NCE
Xét tam giác DMB và tam giác ENC có :
BD = EC (cmt)
^MDB = ^NCE ( cmt )
Vậy tam giác DMB = tam giác ENC ( ch - gn )
=> DM = EN ( 2 cạnh tương ứng )
=> BM = NC ( 2 cạnh tương ứng )
c, Ta có : ^ABM = ^MBC - ^ABC
^ACN = ^NCM = ^ACB
=> ^ABM = ^ACN
Xét tam giác ABM và tam giác ACN có :
AB = AC (gt)
^ABM = ^ACN (cmt)
BM = CN (cmt)
Vậy tam giác ABM = tam giác ACN ( c.g.c )
=> ^AMB = ^ANC ( 2 góc tương ứng )
Xét tam giác AMN có : ^AMB = ^ANC (cmt)
Vậy tam giác AMN cân tại A
Bạn vẽ hình giúp mình nha
a. Tam giác ABC cân tại A nên AB=AC
Ta có: AE=AC+CE, AD=AB+BD
Mà AC=AB, CE=BD
\(\Rightarrow AE=AD\) \(\Rightarrow\Delta ADE\) cân tại A
Xét \(\Delta ADE\) có: \(\dfrac{AB}{BD}=\dfrac{AC}{CE}\)
Áp dụng định lí Ta-let đảo \(\Rightarrow BC//DE\) (đpcm)
Xét \(\Delta BDM\) vuông tại M và \(\Delta CEN\) vuông tại N có:
\(\left\{{}\begin{matrix}BD=CE\\\widehat{MBD}=\widehat{NEC}\left(cùng.bằng.\widehat{ABC}\right)\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta BDM\)=\(\Delta CEN\) \(\Rightarrow\)DM=EN (đpcm)
Kẻ \(AH\perp BC\) \(\left(H\in BC\right)\)
Ta có \(\Delta ABC\) cân tại A nên AH vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow BH=CH\)
Mà MB=CN (\(\Delta BDM\)=\(\Delta CEN\)) \(\Rightarrow AM=AN\)
\(\Rightarrow\Delta AMN\) cân tại A

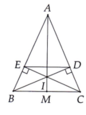

a: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên D là trung điểm của BC
b: Ta có: ΔADC cân tại D
mà DE là đường cao
nên E là trung điểm của AC
TA có: ΔADC vuông tại D
mà DE là đường trung tuyến
nên DE=AC/2=AE
=>ΔEAD cân tại E
mà \(\widehat{DEA}=90^0\)
nên ΔEAD vuông cân tại E