Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

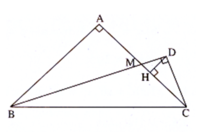
Theo câu a), từ AB = 2AM, suy ra HC = 2HD. Ta có HC < MC (h là chân đường cao hạ từ D của tam giác DCM vuông tại D) nên HC = 2HD < MC = AM < AH (do M nằm giữa A và H), vì thế 2HD không thể bằng AH. Khẳng định b) là sai.

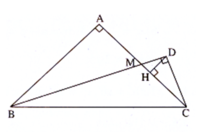
Hai tam giác vuông HCD và DCM đồng dạng (có cùng góc nhọn tại C) mà
∆ DCM ∼ ∆ ABM (vì là hai tam giác vuông có ∠ (DMC) = ∠ (AMB), vậy ∆ HCD ∼ ∆ ABM. Khẳng định a) là đúng.

Ta có: ΔABC cân tại A
mà AD là đường cao ứng với cạnh đáy BC
nên D là trung điểm của BC
Xét ΔBEC có
D là trung điểm của BC
DH//BE
Do đó: H là trung điểm của EC
Xét ΔBEC có
D là trung điểm của BC
H là trung điểm của EC
Do đó: DH là đường trung bình của ΔBEC
Suy ra: \(DH=\dfrac{BE}{2}\)
\(\Leftrightarrow BE=2\cdot DH\)
\(\Leftrightarrow BE^2=4\cdot DH^2\)
\(\Leftrightarrow BE^2=4\cdot AH\cdot CH\)

b: Xét ΔABM vuông tại A có AK là đường cao
nên \(BK\cdot BM=AB^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BK\cdot BM=BH\cdot BC\)