Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC

Hình tự vẽ , giải :
a) Vì \(\Delta ABC\) có \(AB=AC\Rightarrow\Delta ABC\) cân tại A \(\Leftrightarrow\widehat{B}=\widehat{C}\) ( T/c tam giác cân )
Có I nằm trên BC ( vì I là trung điểm BC ) nên có \(\widehat{ABI}=\widehat{ACI}\left(\widehat{B}=\widehat{C}\right)\)
b) Có \(\widehat{B}+\widehat{ABM}=180^0=\widehat{C}+\widehat{ACN}\) ( cặp góc kề bù ). Mà \(\widehat{B}=\widehat{C}\Rightarrow\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\) và \(\Delta ACN\) : \(BM=CN\left(gt\right)\) ; \(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\) ; \(AB=AC\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ACN\left(c.g.c\right)\Leftrightarrow AM=AN\) ( 2 cạnh tương ứng )

a: Xét ΔABC có \(\widehat{B}=\widehat{C}\)
nên ΔABC cân tại A
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN

Xét ΔBHM vuông tại H và ΔCKN vuông tại K có:
BM = CN (gt)
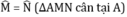
⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
