Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
MA=MC (gt); MB=MQ (gt) => ABCQ là hbh (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)
=> AQ=BC (cạnh đối hbh) (1)
\(\widehat{ABC}=\widehat{AQC}\) (góc đối hbh) (2)
Ta có BL=BC (cạnh hình vuông) (3)
Ta có
\(\widehat{DBL}+\widehat{ABC}=360^o-\widehat{ABD}-\widehat{LBC}=360^o-90^o-90^o=180^o\left(4\right)\)
\(\widehat{BAQ}+\widehat{AQC}=180^o\) (5)
Xét \(\Delta BDL\) và \(\Delta ABQ\) có
BD=AB (cạnh hình vuông)
Từ (1) và (3) => BL=AQ
Từ (2) (4) (5) => \(\widehat{DBL}=\widehat{BAQ}\)
\(\Rightarrow\Delta BDL=\Delta ABQ\) (c.g.c) => DL=BQ
Câu b xem lại đề bài

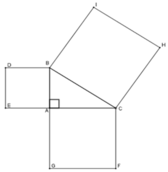
Ta có: SBCHI = BC2; SACFG = AC2; SABDE = AB2
Theo định lý Pytago cho tam giác ABC vuông tại A ta có: BC2 = AB2 + AC2
=> SBCHI = SACFG + SABDE
Đáp án cần chọn là: B
Trên tia đối của tia MB lấy điểm G sao cho BM = MG . Gọi N là trung điểm DL
Dễ dàng chứng minh được BCGA là hình bình hành => AB = CG = BD ;
Ta có : Góc DBL + góc ABC = 360 độ - 90 độ - 90 độ = 180 độ
mà BCGA là hình bình hành => AB // CG => góc ABC + góc GCB = 180 độ
=> góc DBL = góc BCG
Xét tam giác DBL và tam giác BCG có BC = BL (BCKL là hình vuông)
góc DBL = góc BCG (cmt) ; CG = DB
=> tam giác DBL = tam giác BCG (c.g.c)
=> BG = DL => DL = 2BM