Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có DE//BC nên: \(\frac{DA}{DB}=\frac{AE}{CE}\left(1\right)\)
Lại có AB//CG nên: \(\frac{DE}{EG}=\frac{AE}{CE}\left(2\right)\)
Từ (1) và (2) có: ĐPCM
b/Có DE//BC nên
\(\frac{HC}{HE}=\frac{BH}{HG}\left(3\right)\)
Có AB//CG nên
\(\frac{HA}{HC}=\frac{BH}{HG}\left(4\right)\)
Từ (3) và (4) có: \(\frac{HC}{HE}=\frac{HA}{HC}\RightarrowĐPCM\)
c/Ta có: \(\frac{HI}{AB}=\frac{CI}{BC}\left(5\right)\)
Và \(\frac{HI}{CG}=\frac{BI}{BC}\left(6\right)\)
Lấy (5) cộng (6) đước: \(\frac{HI}{AB}+\frac{HI}{CG}=1\Rightarrow\frac{1}{AB}+\frac{1}{CG}=\frac{1}{HI}\)

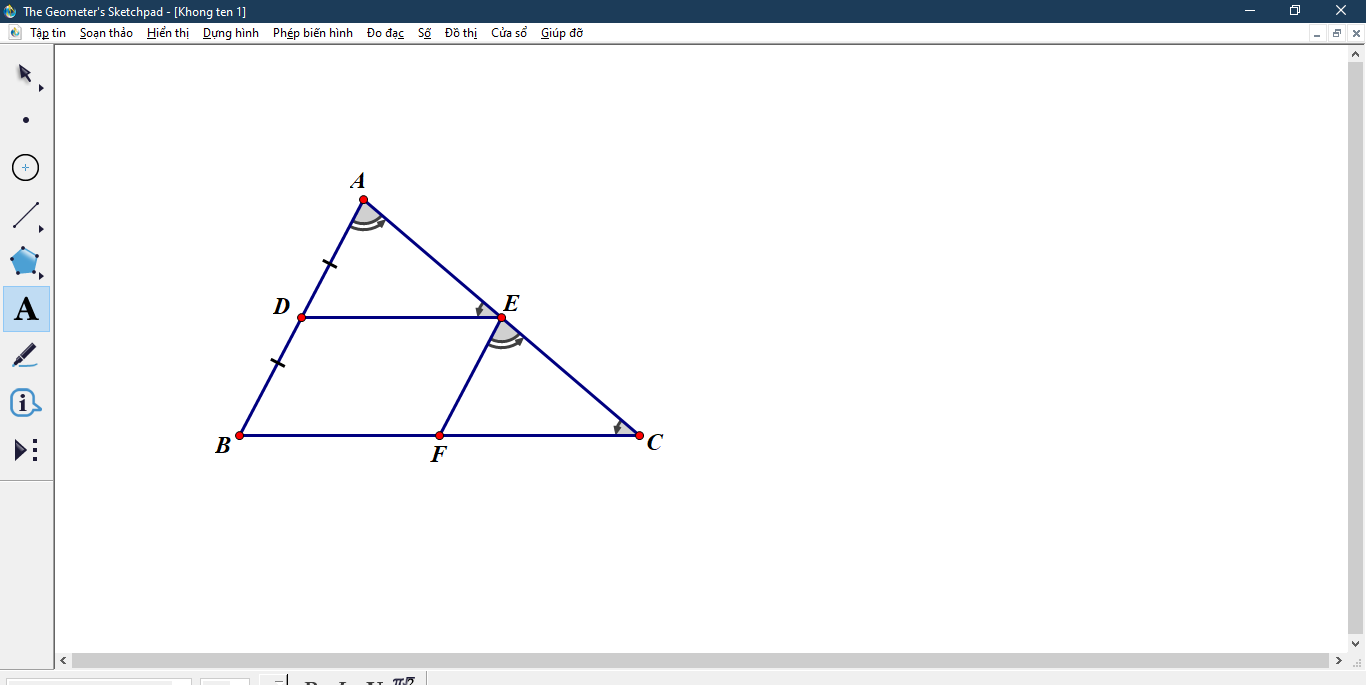
Xét \(\Delta ABC\) có AD=DB;DE//BC nên AE=EC hay E là trung điểm AC
Xét \(\Delta ADE\) và \(\Delta EFC\) có:
\(\left\{{}\begin{matrix}\widehat{DAE}=\widehat{FEC}\\AE=EC\left(cmt\right)\\\widehat{AED}=\widehat{ECF}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ADE\) \(=\) \(\Delta EFC\)\(\left(g.c.g\right)\)
Tick hộ nha
Vì AD=BD và d//BC
=> E là trung điểm của AC
=> AE = EC
Vì DE//BC
=> \(\widehat{AED}=\widehat{ECF}\) (2 góc đồng vị)
Vì ÈF//AB
\(\Rightarrow\widehat{DAE}=\widehat{FEC}\) (2 góc đồng vị)
Xét ΔADE và ΔECF có;
\(\widehat{AED}=\widehat{ECF}\) (cmt)
AE = EC
\(\widehat{DAE}=\widehat{FEC}\) (cmt)
=> ΔADE = ΔECF (g-c-g)