Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Sử dụng định lí Pytago cho các tam giác vuông HAB và HAC để có đpcm
b, 1. Chứng minh tương tự câu a)
2. Sử dụng định lí Pytago cho tam giác vuông AHM

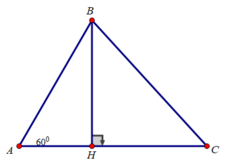
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60 0
BH = AB.sin A = AB.sin 60 0 = (AB 3 )/2
AH = AB.cos A = AB.cos 60 0 = AB/2
Xét tam giác BHC vuông tại H có:
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2
= B H 2 + A C 2 - 2 A C . A H + A H 2
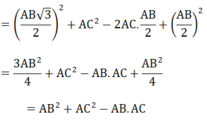
Vậy được điều phải chứng minh.

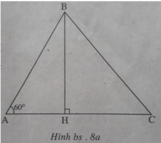
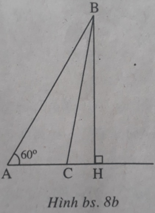
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠ (BAC) = 60 ° là góc nhọn), do đó H C 2 = A C - A H 2 (xem h.bs.8a, 8b)
Công thức Py-ta-go cho ta
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2 = B H 2 + A C 2 + A H 2 - 2 A C . A H = A B 2 + A C 2 - 2 A C . A H
Do ∠ (BAC) = 60 ° nên AH = AB.cos 60 ° = AB/2, suy ra B C 2 = A B 2 + A C 2 - A B . A C



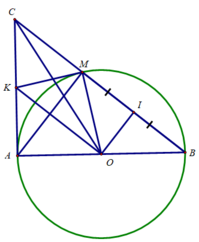
a) Tam giác AMB nội tiếp đường tròn (O) có AB là đường kính
⇒ ΔAMB vuông tại M hay ∠(AMB) = 90o
⇒ AM là đường cao của tam giác ABC
Xét tam giác ABC vuông tại A có AM là đường cao
⇒ A C 2 = CM.CB (hệ thức liên hệ giữa cạnh và đường cao)
kẻ AH\(\perp BC\left(H\in BC\right)\)
ta có: AB2+AC2=AH2+BH2+AH2+HC2
= 2AH2+(MB-MH)2+(MC+MH)2
=2AH2+MB2+MH2-2MB.MH+MC2+MH2+2MC.MH
=2(AH2+MH2)+2MB2(vì MB=MC)
=2AM2+2.\(\frac{BC^2}{4}\)=\(2AM^2+\frac{BC^2}{2}\)(đfcm)
vậy \(AB^2+AC^2=2AM^2+\frac{BC^2}{2}\)