Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Sửa đề: ΔABM=ΔADN
Xét ΔAED và ΔACB có
AE=AC(gt)
\(\widehat{EAD}=\widehat{CAB}\)(hai góc đối đỉnh)
AD=AB(gt)
Do đó: ΔAED=ΔACB(c-g-c)
⇒\(\widehat{ADE}=\widehat{ABC}\)(hai góc tương ứng)
hay \(\widehat{ADN}=\widehat{ABM}\)
Xét ΔADN và ΔABM có
DN=BM(gt)
\(\widehat{ADN}=\widehat{ABM}\)(cmt)
AD=AB(gt)
Do đó: ΔADN=ΔABM(c-g-c)
b) Ta có: ΔADN=ΔABM(cmt)
nên \(\widehat{DAN}=\widehat{BAM}\)(hai góc tương ứng)
mà \(\widehat{BAM}+\widehat{DAM}=180^0\)(hai góc kề bù)
nên \(\widehat{DAN}+\widehat{DAM}=180^0\)
\(\Leftrightarrow\widehat{NAM}=180^0\)
hay M,A,N thẳng hàng(đpcm)

a)
Có: \(AD=AB;AE=AC\)
=> \(\frac{AD}{AB}=1;\frac{AE}{AC}=1\)
=> \(\frac{AD}{AB}=\frac{AE}{AC}=1\)
Áp dụng định lí Talet đảo ta được:
=> DE // BC.
=> \(NDA=ABM\) (2 góc ở vị trí so le trong)
Xét tam giác ABM và tam giác ADN có:
\(\hept{\begin{cases}AB=AD\left(gt\right)\\ABM=ADN\left(cmt\right)\\BM=DN\left(gt\right)\end{cases}}\)
=> Tam giác ABM = Tam giác ADN (cgc)
=> TA CÓ ĐPCM.
b) Do Tam giác ABM = Tam giác ADN (cmt)
=> \(BAM=DAN\)
Áp dụng định lí Talet khi BC // DE ta được:
=> \(\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}\)
Mà: \(\frac{AD}{AB}=\frac{AE}{AC}=1\left(cmt\right)\)
=> \(\frac{DE}{BC}=1\Rightarrow DE=BC\)
Mà: \(BM=DN\left(gt\right)\Rightarrow NE=MC\)
Khi đó, CMTT: Tam giác AMC = Tam giác ANE (cgc)
=> \(MAC=NAE\)
Ta có: \(BAC+ABC+ACB=180\) (ĐỊNH LÍ TỔNG 3 GÓC TRONG TAM GIÁC)
=> \(BAM+MAC+ABC+ACB=180\) (1)
Mà: E, A, C là 3 điểm thẳng hàng
=> góc EAB là góc ngoài của tam giác ABC
=> \(EAB=ABC+ACB\) (2)
Và: \(MAC=EAN\left(cmt\right)\) (3)
TỪ (1); (2) VÀ (3) TA ĐƯỢC:
=> \(BAM+NAE+BAE=180\)
=> \(NAM=180\)
=> 3 điểm M, N, A thẳng hàng.
VẬY TA CÓ ĐPCM.
a) xét \(\Delta ADE\)VÀ \(\Delta ABC\)CÓ
\(AD=AB\left(gt\right);\widehat{DAE}=\widehat{BAC}\left(Đ^2\right);AE=AC\left(gt\right)\)
=> \(\Delta ADE\)=\(\Delta ABC\)(c-g-c)
=> \(\widehat{ADE}=\widehat{ABC}\)( hai góc tương ứng ) hay \(\widehat{ADN}=\widehat{ABM}\)
xét \(\Delta ABM\)VÀ \(\Delta ADN\)CÓ
\(BM=DM\left(gt\right);\widehat{ADN}=\widehat{ABM}\left(cmt\right);AB=AD\left(gt\right)\)
=>\(\Delta ABM\)=\(\Delta ADN\)(c-g-c)
b tối tớ suy nghỉ

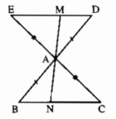
ΔABC và ΔADE có:
AB = AD (gt)
AC = AE (gt)
∠BAC = ∠DAE (hai góc đối đỉnh)
⇒ ΔABC = ΔADE (c.g.c)
⇒ ∠C = ∠E ⇒ DE // BC.

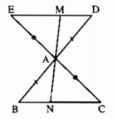
ΔAEM và ΔACN có:
∠C = ∠E ( hai góc so le trong, DE// BC)
AE = AC ( giả thiết)
∠EAM = ∠CAN (hai góc đối đỉnh)
⇒ ΔAEM = ΔACN (g.c.g) ⇒ AM = AN ( hai cạnh tương ứng).
Hình vẽ trước đã !
Xét \(\Delta DEA\) và \(\Delta BAC\) có:
AE=AC( GT)
\(\widehat{DAE}\)=\(\widehat{BAC}\)( Đối đỉnh)
AB= AD( GT)
=> \(\Delta DEA\)=\(\Delta BAC\)( c-g-c)
Khi đó: \(\widehat{EDA}\)=\(\widehat{CBA}\) ( cặp góc tương ứng)
Xét \(\Delta NDA\) và \(\Delta MBA\) có:
DN=BM ( GT)
\(\widehat{EDA}\)=\(\widehat{CBA}\)( C/m trên)
AB=AD( GT)
=>\(\Delta NDA\)=\(\Delta MBA\)( c-g-c)
Khi đó: \(\widehat{BAM}\)=\(\widehat{DAN}\)( cặp góc tương ứng)(1)
Ta có: \(\widehat{DAN}\)+\(\widehat{NAB}\)= 180 độ ( Kề bù)(2)
Kết hợp (1) và (2) suy ra:\(\widehat{BAM}\)+\(\widehat{NAB}\)= 180 độ
Khi đó: \(\widehat{MAN}\)= 180 độ
=> M,A,N thẳng hàng