Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

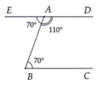
a) Có B A D ^ = A B C ^ ( giả thiết),
Mà hai góc ở vị trí so le trong nên AD // BC (theo tính chất hai đường thẳng song song).
b) Tương tự ý a), chứng minh được AE // BC
Theo tiên đề ơ-clit, hai đường thẳng AE và AD trùng nhau. Từ đó ba điểmD, A, E thẳng hàng.

a) Có B A D ^ = A B C ^ ( giả thiết),
Mà hai góc ở vị trí so le trong nên AD // BC (theo tính chất hai đường thẳng song song).
a) Tương tự ý a), chứng minh
b) được AE // BC
Theo tiên đề ơ-clit, hai đường thẳng AE và AD trùng nhau. Từ đó ba điểm D, A, E thẳng hàng

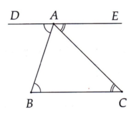
a, Để chứng tỏ DE = 2AM,ta tạo ra đoạn thẳng gấp đôi AM bằng cách lấy K trên tia đối của tia MA sao cho MK = MA,ta sẽ chứng minh AK = DE
Dễ thấy AC = BK, AC // BK . Xét \(\Delta ABK\)và \(\Delta DAE\), ta có :
AB = AD gt
BK = AE cùng bằng AC
\(\widehat{ABK}=\widehat{DAE}\)cùng bù với góc BAC
Do đó \(\Delta ABK=\Delta DAE(c.g.c)\)
\(\Rightarrow AK=DE\)hai cạnh tương ứng
Vậy AM = DE/2
b, Gọi H là giao điểm của MA và DE.Ta có \(\widehat{BAK}+\widehat{DAH}=90^0\)nên \(\widehat{D}+\widehat{DAH}=90^0\), do đó góc AHD = 900