Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

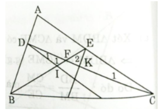
Gọi F là giao điểm của BE và CD.
Ta có DI // AC (gt) ⇒ ∠D1 = ∠C1 (so le trong)
và ∠F1 = ∠F2 (đối đỉnh)
Do đó: ΔDFI ∼ ΔCFE (g.g)
![]()
Tương tự ta có: ΔDFB ∼ ΔKFE
![]()
Từ (1), (2) ⇒ FC.FI = FB.FK
![]()
Do đó theo định lí Talét đảo ta có KI // BC.

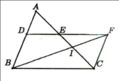
a/ Xét tg DIE và tg CID có
\(\widehat{CDE}=\widehat{BCD}\) (góc so le trong)
\(\widehat{BED}=\widehat{CBE}\) (góc so le trong)
=> tg DIE đồng dạng tg CID (g.g.g)
b/
Ta có DE//BC
Xét tg ABM có \(\dfrac{DN}{BM}=\dfrac{AN}{AM}\) (1)
Xét tg ACM có \(\dfrac{EN}{CM}=\dfrac{AN}{AM}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{DN}{BM}=\dfrac{EN}{CM}\) mà BM=CM => DN=EN
c/
Nôi A với I cắt DE tại N'; cắt BC tại M'
Ta có
\(\dfrac{DN'}{CM'}=\dfrac{IN'}{IM'}\)
\(\dfrac{EN'}{BM'}=\dfrac{IN'}{IM'}\)
\(\Rightarrow\dfrac{DN'}{CM'}=\dfrac{EN'}{BM'}\) (1)
Ta có
\(\dfrac{EN'}{CM'}=\dfrac{AI}{AM'}\)
\(\dfrac{DN'}{BM'}=\dfrac{AI}{AM'}\)
\(\Rightarrow\dfrac{EN'}{CM'}=\dfrac{DN'}{BM'}\) (2)
Công 2 vế của (1) và (2)
\(\dfrac{DN'+EN'}{CM'}=\dfrac{EN'+DN'}{BM'}\Rightarrow\dfrac{DE}{CM'}=\dfrac{DE}{BM'}\)
=> CM' = BM' => M' là trung điểm của BC => M trùng M'
Từ (1) => DN'=EN' => N' là trung điểm của DE mà N là trung điểm của DE => N trùng N'
=> N; I; M thẳng hàng

9+9=18