Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔDEB có
P là trung điểm của DE
Q là trung điểm của BE
Do đó: PQ là đường trung bình của ΔDEB
Suy ra: PQ//DB và \(PQ=\dfrac{DB}{2}\left(1\right)\)
Xét ΔDCB có
N là trung điểm của CD
M là trung điểm của BC
Do đó: NM là đường trung bình của ΔDCB
Suy ra: NM//DB và \(NM=\dfrac{DB}{2}\left(2\right)\)
Từ (1) và (2) suy ra NM//PQ và NM=PQ
hay NMQP là hình bình hành
tam giác BDE: M là tđ(trung điểm) DE, N là tđ BE => MN là đtb(đường trung bình) của tam giác BDE.=> MN//DB <=> MN//BA
tương tự c/m MQ là đtb của tam giác DEC=> MQ//EC hay MQ//AC. mà AC vuông góc AB=> MN vuông góc PQ.=> góc NMQ =90. tương tự theo cách đtb thì các góc còn lại của tứ giác MNPQ =90=> là hình chữ nhật
MN là đtb=> MN=1/2 DB. MQ=1/2 EC mà EC=DB=> MN=DB
=> tg là hình vuông(dhnb)
lần sau vẽ hình nha! làm bài đã dài r lại còn phải vẽ hình nữa :(
Đọc tiếpĐúng 0Bình luận (2)
vũ tiến đạt12 tháng 11 2017 lúc 12:52 ta có hình vẽ
a) Do P là trung điểm của DE (gt), Q là trung điểm của BE (gt) nên PQ là đường trung bình của tam giác BED, suy ra PQ=1/2BD.
Chứng minh tương tự MN =1/2 BD, NP = 1/2CE và MQ = 1/2CE.
Mặt khác BD = CE (gt)
Do đó MN = NP = PQ = QM
Vậy tứ giác MNPQ là hình thoi.
b) Do PN // AC, PQ // AB nên (hai góc có cạnh tướng ứng song song).
Gọi giao điểm của MP với AB là R, ta có ...
Phùng Khánh Linh12 tháng 11 2017 lúc 12:55
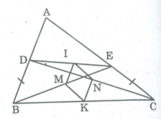
*Trong ∆ BCD,ta có:
K là trung điểm của BC (gt)
N là trung điểm của CD (gt)
Nên NK là đường trung bình của ∆ BCD
⇒ NK // BD và NK = 1/2 BD (1)
*Trong ∆ BED,ta có:
M là trung điểm của BE (gt)
I là trung điểm của DE (gt)
Nên MI là đường trung bình của ∆ BED
⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)
Từ (1) và (2) suy ra: MI // NK và MI = NK
Nên tứ giác MKNI là hình bình hành.
*Trong ∆ BEC ta có MK là đường trung bình.
⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)
BD = CE (gt). Suy ra: MK = KN
Vậy hình bình hành MKNI là hình thoi.
⇒IK ⊥ MN (t/chất hình thoi).
Áp dụng định lí về đường trung bình của tam giác để chứng minh MI = IN = NK = KM (cùng bằng \(\dfrac{BD}{2}\) và \(\dfrac{CE}{2}\) )
MINK là hình thoi nên \(IK\perp MN\)
