K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
26 tháng 10 2019
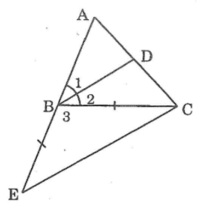
Ta có: BD là tia phân giác của ∠ABC (giả thiết)
Suy ra: 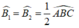 (1)
(1)
Lại có: BE = BC (giả thiết)
=>∆BEC cân tại B (theo định nghĩa)
Suy ra: ∠E= ∠BCE (tính chất tam giác cân)
∆BEC có ABC là góc ngoài đỉnh B
=>∠ABC= ∠E + ∠BCE (tính chất góc ngoài tam giác)
Suy ra: ∠ABC=2∠E
Hay ∠E = (1/2)∠ABC (2)
Từ (1) và (2) suy ra: ∠E = ∠B1 = (1/2)∠ABC
Vậy BD // CE (vì có cặp góc ở vị trí đồng vị bằng nhau)
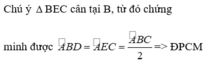
\(\Delta EBCcó:BE=BC\left(gt\right)\)
\(\Rightarrow\Delta EBC\) cân tại B
\(\Rightarrow\) góc E = góc C
Ta có : góc ABD + góc DBC + góc CBE = 1800 (kề bù)
\(\Rightarrow\) góc CBE = 1800 - ( góc ABD + góc DBC)
Và ta lại có: góc E + góc CBE + góc C = 1800 (tổng 3 góc trong tam giác EBC)
\(\Rightarrow\) góc CBE = 1800 - ( góc E + góc C)
Mà : góc ABD = góc DBC ( vì BD là tia phân giác của góc ABC)
góc E = C ( cmt )
\(\Rightarrow\) góc DBC = góc C
Mà : 2 góc này nằm ở vị trí so le trong
\(\Rightarrow BDsong^2EC\)