Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc BFE+góc BCE=180 độ
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
b: Xét tứ giác BFHD có
góc BFH+goc BDH=180 độ
=>BFHD là tứ giác nội tiếp
Xét tứ giác CEHD có
góc CEH+góc CDH=180 độ
=>CEHD là tứ giác nội tiếp
góc FDH=góc FBH
góc EDH=góc ACF
mà góc FBH=góc ACF
nên góc FDH=góc EDH
=>DH là phân giác của góc FDE(1)
góc EFH=góc CAD
góc DFH=góc EBC
mà góc CAD=góc EBC
nên góc EFH=góc DFH
=>FH là phân giác của góc EFD(2)
Từ (1), (2) suy ra H là giao của ba đường phân giác của ΔDEF
c: Xét ΔBHD vuông tại D và ΔBCE vuông tại E có
góc HBD chung
=>ΔBHD đồg dạng với ΔBCE
=>BH/BC=BD/BE
=>BH*BE=BC*BD
Xét ΔCDH vuông tại Dvà ΔCFB vuông tại F có
góc FCB chung
=>ΔCDH đồng dạng với ΔCFB
=>CD/CF=CH/CB
=>CD*CB=CH*CF
=>BH*BE+CH*CF=BC^2

Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)
Do đó: ΔFHB\(\sim\)ΔEHC
Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
\(\widehat{DBH}\) chung
Do đó: ΔBDH\(\sim\)ΔBEC
Suy ra: BD/BE=BH/BC
hay \(BD\cdot BC=BE\cdot BH\)

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAC}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)

bạn vẽ hình nha.
a) tg AFC và tg AEB có :
góc A chung
góc AEB = góc AFC (=90 do)
=> tg AFC ~tg AEB (g.g)
=>\(\frac{AF}{AE}=\frac{AC}{AB}\) =>AB.AF=AE.AC
b) ta có AB.AF=AE.AC => \(\frac{AF}{AC}=\frac{AE}{AB}\)
tg AEF và tg ABC có
góc A chung
\(\frac{AF}{AC}=\frac{AE}{AB}\)
=> tg AEF ~tg ABC (c.g.c)
c) từ H vẽ HI vuông góc vs BC tại I
tg BHI và tg BCE có:
góc HBC chung
góc BHI= góc BEC
=>tg BHI ~ tg BCE (g.g)
=>\(\frac{BH}{BC}=\frac{BI}{BE}\) => BH.BE=BC.BI (1)
tg CHI và tg CBF có:
góc FCB chung
góc HIC= góc BFC
=> tg CHI ~ tg CBF(g.g)
=>\(\frac{CH}{CB}=\frac{CI}{CF}\) => CH.CF=BC.CI (2)
từ (1) và (2) , cộng vế theo vế, ta được
BH.BE+CH.CF=BC.BI+BC.CI
=>BH.BE+CH.CF=BC(BI+CI)
=>BH.BE+CH.CF=\(BC^2\)

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC
b: Ta có: ΔAEB\(\sim\)ΔAFC
nên AE/AF=AB/AC
hay AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
\(\widehat{EAF}\) chung
DO đó: ΔAEF\(\sim\)ΔABC

a) xét tam giác ABD và tam giác AHF có
góc BAD chung
Góc AFH = góc ADB (=90 độ)
=> tam giác ABD đồng dạng vs tam giác AHF (g.g)
=> AB/AD = AH/AF
=> AF.AD = AH.AD
b) xét tam giác AFC và tam giác AEB có
Góc A chung
Góc AFC = góc AEB (=90 độ)
=> tam giác AFC đồng vs tam giác AEB (g.g)
=> AF/AC = AE/AB
=> AF.AB= AE.AC
a: Xét ΔABD vuông tại D và ΔAHF vuông tại F có
góc FAH chung
=>ΔABD đồng dạng với ΔAHF
=>AB/AH=AD/AF
=>AB*AF=AH*AD
b: Xet ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
=>AE/AB=AF/AC
=>ΔAEF đồng dạng với ΔABC
c:góc FEC=góc DAC
góc DFC=góc EBC
mà góc DAC=góc EBC
nên góc FEC=goc DFC
=>FC là phân giác của góc EFD
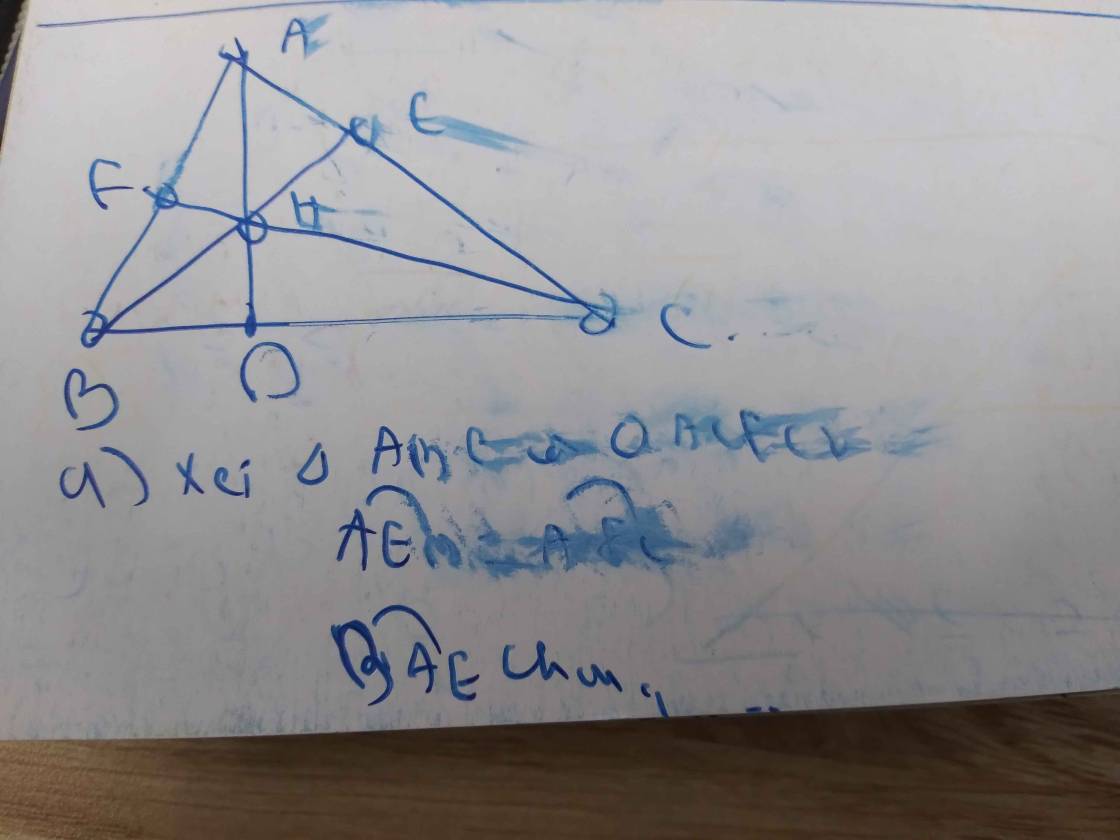


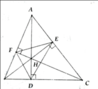
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
Do đó: ΔABE\(\sim\)ΔACF
Suy ra: AB/AC=AE/AF
hay \(AB\cdot AF=AC\cdot AE\)
b: Xét ΔAFE và ΔACB có
AF/AC=AE/AB
góc FAE chung
Do đó: ΔAFE\(\sim\)ΔACB
c: Gọi K là giao điểm của AH với BC
=>AK vuông góc với BC tại K
Xét ΔBFH vuông tại F và ΔBEA vuông tại E có
góc FBH chung
Do đó:ΔBFH\(\sim\)ΔBEA
Suy ra: BF/BE=BH/BA
hay \(BF\cdot BA=BE\cdot BH\)
Xét ΔCEH vuông tại E và ΔCFA vuông tại F có
góc FCA chung
Do đó: ΔCEH\(\sim\)ΔCFA
Suy ra: CE/CF=CH/CA
hay \(CH\cdot CF=CE\cdot CA\)
Xét ΔBFC vuông tại F và ΔBKA vuông tại K có
góc KBA chung
Do đó: ΔBFC\(\sim\)ΔBKA
Suy ra: BF/BK=BC/BA
hay \(BF\cdot BA=BK\cdot BC\)
Xét ΔCEB vuông tại E và ΔCKA vuông tại K có
góc ECB chung
Do đó:ΔCEB\(\sim\)ΔCKA
Suy ra: CE/CK=CB/CA
hay \(CE\cdot CA=CB\cdot CK\)
\(BH\cdot BE+CH\cdot CF=BF\cdot BA+CE\cdot CA\)
\(=BC\cdot BK+BC\cdot CK=BC^2\)