K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DM
24 tháng 3 2022
Giải thích các bước giải:
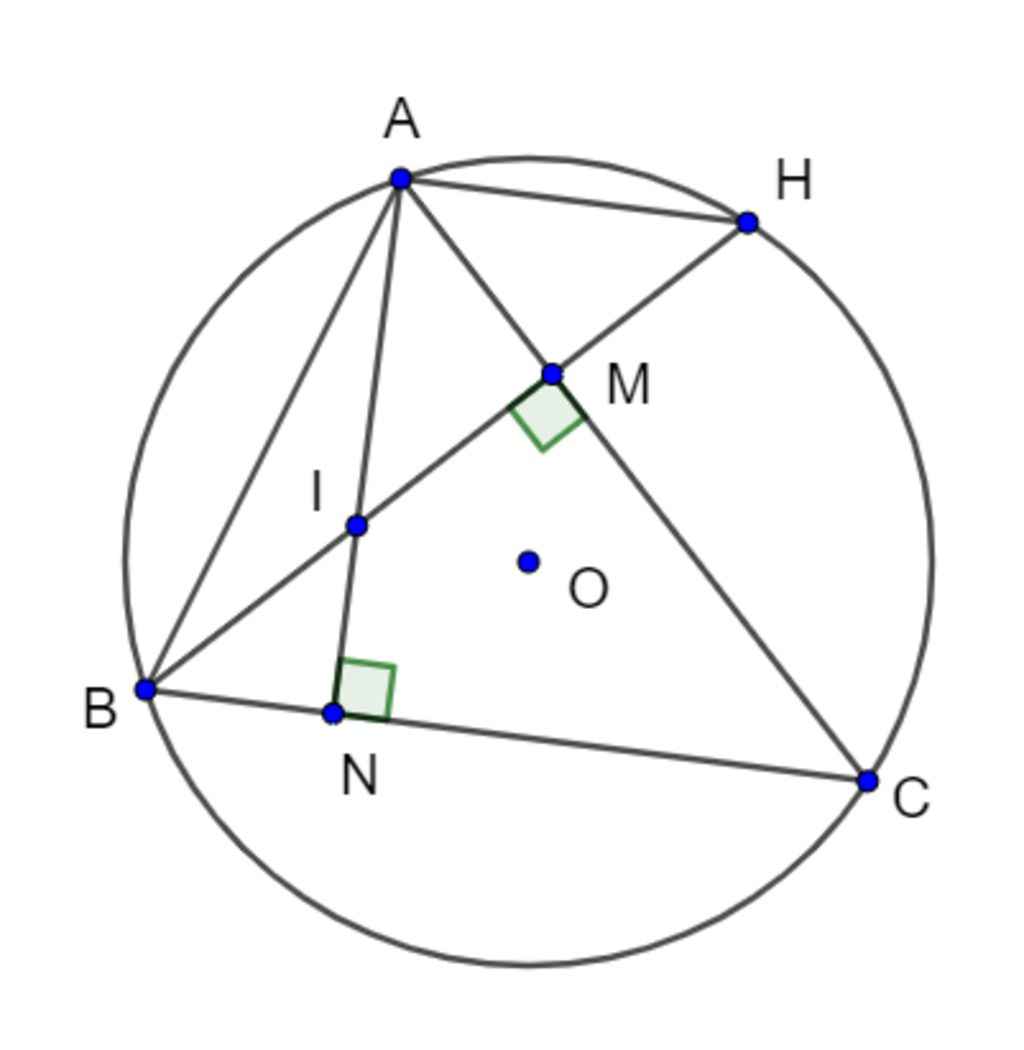
a) ΔABCΔABC có đường cao AN,BMAN,BM
⇒AN⊥BC;BM⊥AC⇒AN⊥BC;BM⊥AC
Xét tứ giác IMCNIMCN có:
ˆIMC=ˆINC=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)IMC^=INC^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
⇒ˆIMC+ˆINC=1800⇒IMC^+INC^=1800
⇒⇒ tứ giác IMCNIMCN nội tiếp
b) Xét ΔBINΔBIN và ΔAIMΔAIM có:
ˆBNI=ˆAMI=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)BNI^=AMI^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
ˆBIN=ˆAIMBIN^=AIM^ (đối đỉnh)
⇒⇒ ΔBIN∽ΔAIMΔBIN∽ΔAIM (g.g)
⇒IBIA=INIM⇒IA.IN=IM.IB⇒IBIA=INIM⇒IA.IN=IM.IB
c) Tứ giác IMCNIMCN nội tiếp
⇒ˆAIH=ˆNCM⇒AIH^=NCM^ hay ˆAIH=ˆACBAIH^=ACB^
Xét (O)(O) có: ˆACB=ˆAHBACB^=AHB^ (2 góc nội tiếp cùng chắn cung ABAB)
⇒ˆAIH=ˆAHB⇒AIH^=AHB^
⇒ˆAIH=ˆAHI⇒ΔAIH⇒AIH^=AHI^⇒ΔAIH cân tại A⇒AI=AH
