Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
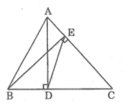
a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{BAE}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC
b: Ta có: ΔAEB\(\sim\)ΔAFC
nên AE/AF=AB/AC
hay AE/AB=AF/AC
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
\(\widehat{EAF}\) chung
DO đó: ΔAEF\(\sim\)ΔABC
Xét △ ADC và △ BEC, ta có:
∠ (ADC) = ∠ (BEC) = 90 0
∠ C chung
Suy ra: △ ADC đồng dạng △ BEC (g.g)
Suy ra: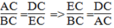
⇒ ECBC = DCAC
Xét △ DEC và △ ABC ta có:
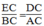
∠ C chung
Vậy △ DEC đồng dạng △ ABC (c.g.c)
a: Xét ΔAEBvuông tại E và ΔAFC vuông tại F co
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
b: ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE/AB=AF/AC
=>ΔAEF đồng dạng với ΔABC
a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
Do đó: ΔCDA\(\sim\)ΔCEB
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)
Do đó: ΔHEA\(\sim\)ΔHDB
Suy ra: HE/HD=HA/HB
hay \(HE\cdot HB=HD\cdot HA\)
Xét ∆AHE và ∆BHD, ta có
<D=<E=90°
<BHD=<EHA ( đối đỉnh)
⟹ ∆AHE ∼∆BHD(g.g)
⟹HA/HB=HE/HD⟹ HA*HD=HB*HE
