Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Dễ dàng chứng minh bằng cách áp dụng hệ thức về cạnh trong các tam giác vuông ABD và ACD :
\(AE.AB=AF.AC=AD^2\)
b/ Bạn tham khảo ở đây nhé : http://olm.vn/hoi-dap/question/633787.html
c/ Áp dụng tứ giác nội tiếp để giải (liên quan đến góc ngoài của tứ giác nội tiếp)

a) Ta có A, E, F, K, H cùng thuộc đường tròn đường kính AH.
b) Ta có \(\widehat{AMN}=90^o-\widehat{OAB}=90^o-\dfrac{180^o-\widehat{AOB}}{2}=\dfrac{\widehat{AOB}}{2}=\widehat{ACB}\).
Suy ra tứ giác BMNC nội tiếp và \(\Delta SMB\sim\Delta SCN\left(g.g\right)\) nên \(SM.SN=SB.SC\).
c) Ta có \(\widehat{QCB}=\widehat{QAB}=\widehat{HCB};\widehat{QBC}=\widehat{HBC}\) nên Q, H đối xứng với nhau qua BC.
Mà S thuộc BC nên SH = SQ.
Ta lại có \(\widehat{SHB}=\widehat{BHF}-\widehat{MHF}=\widehat{BAC}-\left(90^o-\widehat{AMH}\right)=\widehat{BAC}+\widehat{ACB}-90^o=90^o-\widehat{ABC}=\widehat{SCH}\Rightarrow\Delta SHB\sim\Delta SCH\left(g.g\right)\Rightarrow SQ^2=SH^2=SB.SC\).
d) I là điểm nào vậy bạn?

Chọn đáp án D

* Chứng minh các tứ giác ABHF và BMFO nội tiếp.
- Từ giả thiết suy ra: 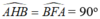
=> H và F thuộc đường tròn đường kính AB (quỹ tích cung chứa góc)
Vậy tứ giác ABHF nội tiếp đường tròn đường kính AB
- Gọi M là trung điểm của BC (gt), suy ra: OM ⊥ BC
Khi đó: 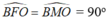
Nên M, F thuộc đường tròn đường kính OB(quỹ tích cung chứa góc).
Vậy tứ giác BMOF nội tiếp đường tròn đường kính OB
* Chứng minh HE // BD.
Dễ chứng minh tứ giác ACEH nội tiếp đường tròn đường kính AC.
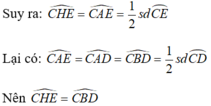
Và chúng ở vị trí so le trong suy ra: HE // BD

a)
Xét (O) có
M là trung điểm của dây BC(gt)
nên OM\(\perp\)BC(Định lí đường kính vuông góc với dây)
Xét tứ giác BMOF có
\(\widehat{BFO}+\widehat{BMO}=180^0\left(90^0+90^0=180^0\right)\)
nên BMOF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: BC=10cm
=>AH=6*8/10=4,8cm
b: ΔAHB vuông tại H
mà HM là trung tuyến
nên HM=AM
Xét ΔOAM và ΔOHM có
OA=OH
MA=MH
OM chung
Do đó: ΔOAM=ΔOHM
=>góc OHM=90 độ
=>MH là tiếp tuyến của (O)