Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tớ làm hơi qua loa một chút phần nào có kí hiệu t là tớ hơi tắt chút xíu nhé ( ko mún viết nhìu )
hình cậu tự vẽ nhá !
a)xét tam giác ABD và tam giác ACE ta có : góc a chung ; góc BDA=góc CEA =90 độ suy ra tam giác ABD đồng dạng với tam giác ACE theo trường hợp góc-góc
b) theo a) ta có tam giác ABD đồng dạng với tam giác ACE\(\Rightarrow\)\(\frac{AD}{AE}=\frac{AB}{AC}\)(t)
xét tam giác AED và tam giác ACB ta có góc a chung ; (t) ta suy ra tam giác AED đồng dạng với tam giác acb theo trường hợp cạnh-góc-cạnh suy ra gócAED=gócACB=40độ
nhớ k cho mk nha!

Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔABD∼ΔACE
Suy ra: AB/AC=AD/AE
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
\(\widehat{DAE}\) chung
Do đó: ΔADE∼ΔABC
Suy ra: \(\widehat{AED}=\widehat{ACB}=48^0\)

a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE; AD/AB=AE/AC
c: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
=>góc AED=góc ACB

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
=>ΔABD đồng dạng với ΔACE
b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: góc A=90-30=60 độ
ΔADE đồng dạng với ΔABC
=>S ADE/S ABC=(AD/AB)^2=1/4
=>S ABC=120cm2

a. -Xét △BEH và △CDH có:
\(\widehat{BEH}=\widehat{CDH}=90^0\)
\(\widehat{BHE}=\widehat{CHD}\)(đối đỉnh)
\(\Rightarrow\)△BEH∼△CDH (g-g).
\(\Rightarrow\dfrac{BH}{CH}=\dfrac{EH}{DH}\).
-Xét △HED và △HBC có:
\(\widehat{EHD}=\widehat{BHC}\) (đối đỉnh)
\(\dfrac{BH}{CH}=\dfrac{EH}{DH}\left(cmt\right)\)
\(\Rightarrow\)△HED∼△HBC (c-g-c).
b. -Ta có: \(\widehat{AED}+\widehat{DEC}=90^0\) (kề phụ).
\(\widehat{DBC}+\widehat{DCB}=90^0\) (△DBC vuông tại D).
Mà \(\widehat{DEC}=\widehat{DBC}\)(△HED∼△HBC)
\(\Rightarrow\)\(\widehat{AED}=\widehat{DCB}\)
-Xét △AED và △ACB có:
\(\widehat{AED}=\widehat{ACB}\) (cmt)
\(\widehat{BAC}\) là góc chung.
\(\Rightarrow\)△AED∼△ACB (g-g).
c. -Có: \(\widehat{EAC}=45^0\) (gt) ; △AEC vuông tại E (AB⊥CE tại E).
\(\Rightarrow\)△AEC vuông cân tại E.
\(\Rightarrow AE=AC\sqrt{2}\)
-Ta có: △AED∼△ACB (cmt)
\(\Rightarrow\dfrac{ED}{BC}=\dfrac{AE}{AC}=\dfrac{AC\sqrt{2}}{AC}=\sqrt{2}\)
\(\Rightarrow\dfrac{ED}{\sqrt{2}}=\sqrt{2}\)
\(\Rightarrow ED=2\)

Xét \(\Delta AEC\&\Delta ADB\\ \) có:
\(\widehat{A}=\widehat{A}\\ \widehat{E}=\widehat{D}=90^o\\ \Rightarrow\Delta AEC\sim\Delta ADB\left(đpcm\right)\)
b) vì\(\Delta AEC\sim\Delta ADB\Leftrightarrow\dfrac{AB}{AE}=\dfrac{AC}{AD}\Leftrightarrow\dfrac{3}{AE}=\dfrac{5}{2}\Rightarrow AE=\dfrac{3\cdot2}{5}=1.2cm\)
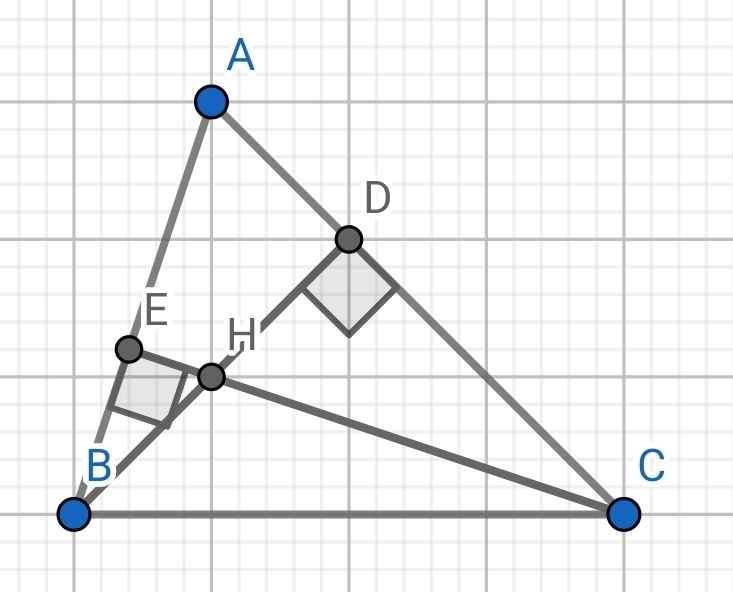
a) Xét ∆ADB và ∆ACE có:
∠ADB = ∠ACE = 90⁰
∠A chung
⇒ ∆ADB ∽ ∆ACE (g-g)
b) Do ∆ADB ∽ ∆ACE (cmt)
⇒ AD/AC = AB/AE
⇒ AE = AB.AC/AD
= 2.3/5
= 1,2 (cm)
