Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB
ΔANB vuông tại N có NE vuông góc AB
nên AN^2=AE*AB
ΔAMC vuông tại M có MD vuông góc AC
nên AM^2=AD*AC
=>AN=AM

Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE
Xet ΔAMC vuông tại M có MD là đường cao
nên AD*AC=AM^2
Xét ΔANB vuông tại N có NE là đường cao
nên AE*AB=AN^2
=>AN=AM
=>ΔAMN cân tại A

hinh bn tu ve nhe
\(\infty:\)dong dang
\(\Delta ABD\infty\Delta ACE\)(g.g) \(\Rightarrow\frac{AE}{AD}=\frac{AC}{AB}\)
\(\Rightarrow AE.AB=AD.AC\) (1)
\(\Delta AMB\infty\Delta AEM\)(g.g) \(\Rightarrow\frac{AM}{AE}=\frac{AB}{AM}\Rightarrow AM^2=AE.AB\)(2)
\(\Delta ANC\infty\Delta ADN\)(g.g) \(\Rightarrow\frac{AN}{AD}=\frac{AC}{AN}\Rightarrow AN^2=AD.AC\)(3)
Tu (1), (2), (3) \(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
\(\Rightarrow\)\(\Delta AMN\)can tai A

1: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
2: Xet ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
3: ΔAMC vuông tại M có MD vuông góc AC
nên AD*AC=AM^2
ΔANB vuông tại N có NE vuông góc AB
nên AE*AB=AN^2
=>AM=AN

1.
a. CN và BM cùng vuông góc DE nên CN//BM
\(\Rightarrow\) BMNC là hình thang vuông tại M và N
b. Theo giả thiết BD vuông góc CA \(\Rightarrow\Delta BDC\) vuông tại D
\(\Rightarrow DO\) là trung tuyến ứng với cạnh huyền BC \(\Rightarrow DO=\dfrac{1}{2}BC\)
Tương tự trong tam giác vuông BEC thì EO là trung tuyến ứng với cạnh huyền
\(\Rightarrow EO=\dfrac{1}{2}BC\Rightarrow DO=EO\Rightarrow\) tam giác cân tại O
c. Tam giác DEO cân tại O, mà P là trung điểm DE \(\Rightarrow OP\) là trung tuyến đồng thời là đường cao
\(\Rightarrow OP\perp DE\) \(\Rightarrow OP//CN//BM\)
Mà O là trung điểm BC \(\Rightarrow OP\) là đường trung bình hình thang BMNC
\(\Rightarrow OP=\dfrac{CN+BM}{2}\)
2. Đặt biểu thức là A
Với \(p=2\) ko thỏa mãn
Với \(p=3\Rightarrow A=71\) là SNT
Với \(p>3\) do p là SNT nên p chỉ có 2 dạng \(p=3k+1\) hoặc \(3k+2\)
- Với \(p=3k+1\Rightarrow p^3\) chia 3 dư 1, \(p^2\) chia 3 dư 1, \(11p=9p+2p\) chia 3 dư 2
\(\Rightarrow A\) chia 3 dư 1+1+2+2=6 chia hết cho 3 (ko là SNT) loại
- Với \(p=3k+2\) tương tự, \(p^3\) chia 3 dư 2, \(p^2\) chia 3 dư 1, \(11p\) chia 3 dư 1
\(\Rightarrow\) A chia 3 dư 2+1+1+2=6 vẫn chia hết cho 3 (loại)
Vậy \(p=3\) là giá trị duy nhất thỏa mãn
Em cảm ơn anh nhiều ạ . Anh có thể cho e xin cách làm bài 2 được k ạ
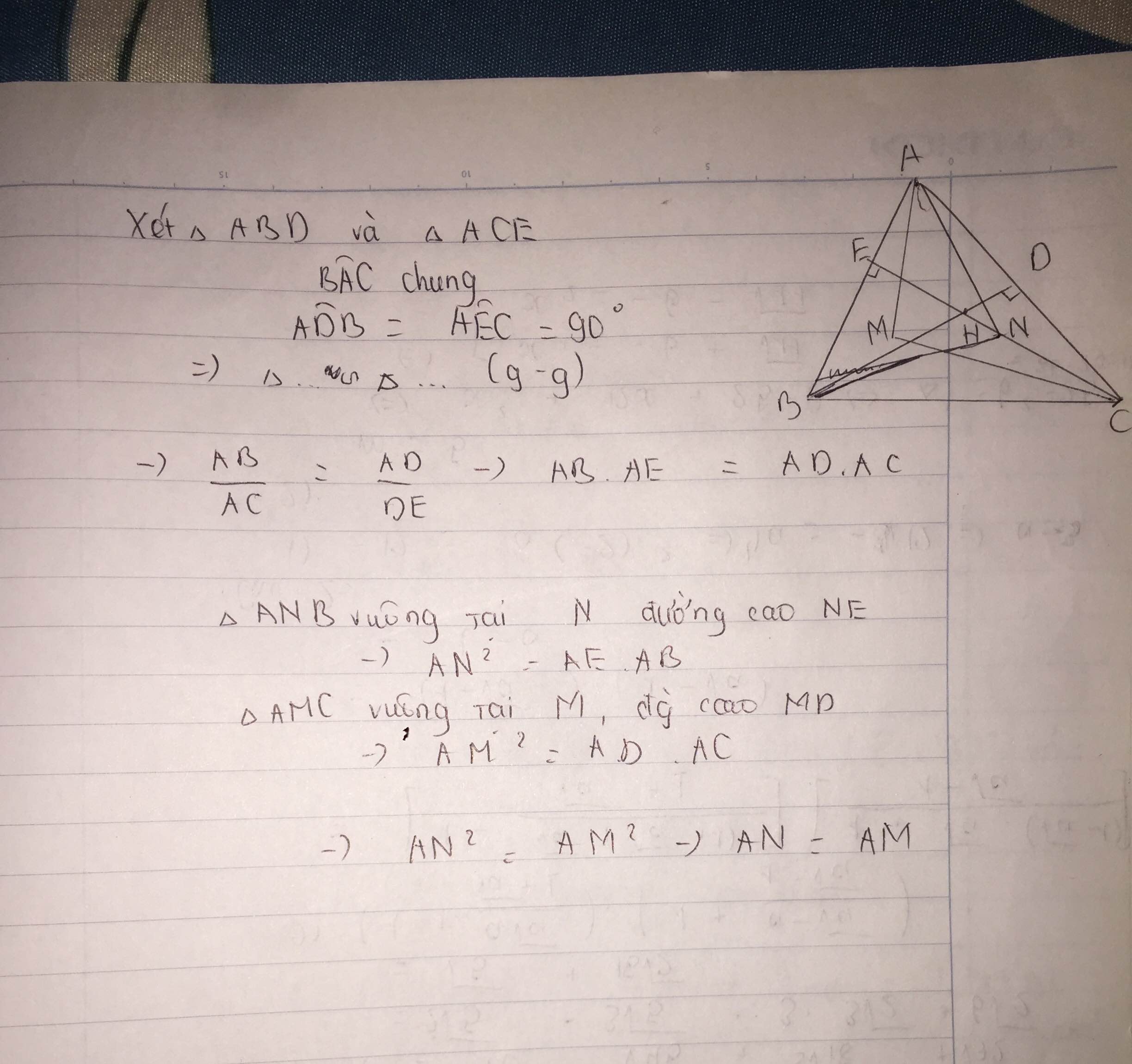
b nào bít thi giup nke. mình dang cần gấp!!!