Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tg AEHF co E=F=90( o vi tri goc doi)
nen AEHF la tg noi tiep
b) tớ chua ve hinh nên bạn tu lam neu k dc
tớ lam tiep

a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}\)
nên BFEC là tứ giác nội tiếp

c: Vì góc B là góc nội tiếp chắn cung nhỏ AC
nên \(sđ\stackrel\frown{AC}=2\cdot\widehat{B}=120^0\)

c.
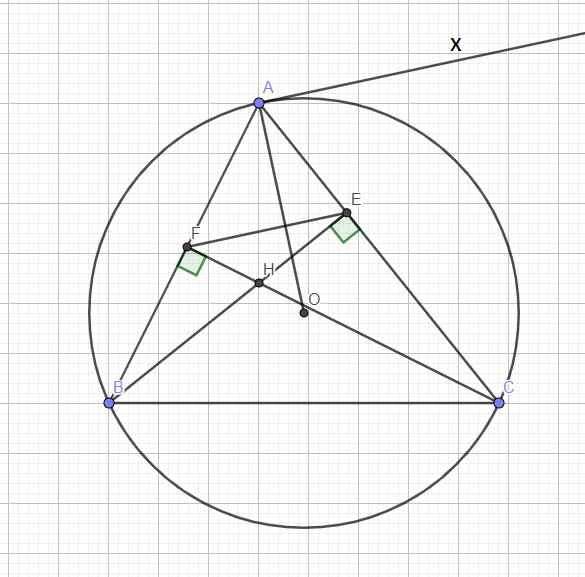
Qua A kẻ tiếp tuyến \(Ax\Rightarrow Ax\perp OA\) (1)
Do E và F cùng nhìn BC dưới 1 góc vuông
\(\Rightarrow\) Tứ giác BCEF nội tiếp
\(\Rightarrow\widehat{CEF}+\widehat{CBF}=180^0\)
Mà \(\widehat{CEF}+\widehat{AEF}=180^0\)
\(\Rightarrow\widehat{CBF}=\widehat{AEF}\)
Lại có \(\widehat{CBF}=\widehat{CAx}\) (cùng chắn AC)
\(\Rightarrow\widehat{AEF}=\widehat{CAx}\)
\(\Rightarrow Ax||EF\) (hai góc so le trọng bằng nhau) (2)
\(\left(1\right);\left(2\right)\Rightarrow OA\perp EF\)

a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b; góc ABD=1/2*180=90 độ
=>BD vuông góc AB
=>BD//CH
góc ACD=1/2*180=90 độ
=>CD vuông góc AC
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hbh
=>BC cắt HDtại trung điểm của mỗi đường
=>H,M,D thẳng hàng

a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC

a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
b: \(sđ\stackrel\frown{AC}=2\cdot60^0=120^0\)