Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
b: góc EDH=góc BAF
góc FDH=góc ECB
mà góc BAF=góc ECB
nên góc EDH=góc FDH
=>DH là phân giác của góc EDF

a: Xét tứ giác ADHE có
góc AdH+góc AEH=180 độ
=>ADHElà tứ giác nội tiếp
I là trung điểm của AH
b: Xét tứ giác BEDC có
góc BEC=góc BDC=90 độ
=>BEDC là tứ giác nội tiếp
góc EDB=góc BAF
góc FDB=góc ECB
mà góc BAF=góc ECB
nên góc EDB=góc FDB
=>DB là phân giác của góc EDF

a ) Ta có : \(BD\perp AC,CE\perp AB\)
\(\Rightarrow\widehat{ADH}=\widehat{AEH}=90^0,\widehat{BDC}=\widehat{BEC}=90^0\)
\(\Rightarrow ADHE,BEDC\) nội tiếp
b . Ta có : \(\widehat{DHC}=\widehat{EHB},\widehat{HDC}=\widehat{HEB}=90^0\)
\(\Rightarrow\Delta HDC~\Delta HEB\left(g.g\right)\)
\(\Rightarrow\frac{HD}{HE}=\frac{HC}{HB}\Rightarrow HD.HB=HE.HC\)
c . Vì H là trực tâm \(\Delta ABC\Rightarrow AH\perp BC=F\)
Lại có : \(\widehat{AHD}=\widehat{CBF}\left(+\widehat{FAC}=90^0\right)\)
\(\widehat{AID}=\widehat{ACB}\Rightarrow\widehat{AID}=\widehat{AHD}\)
\(\Rightarrow\Delta AHI\) cân tại A
Mà \(AD\perp HI\Rightarrow AD\) là trung trực của HI \(\Rightarrow\)AC là đường trung trực của của HI.
d ) Từ câu c \(\Rightarrow AI=AH\)
Tương tự \(\Rightarrow AK=AH\Rightarrow A\) là tâm đường tròn ngoại tiếp \(\Delta HIK\)

a) Tứ giác BEHK có hai góc đỉnh E, K là vuông nên bốn đỉnh của tứ giác thuộc đường tròn đường kính EK.
Mặt khác, tứ giác ABKD có bốn đỉnh nằm trên đường tròn đường kính AB. Theo tính chất về các góc nội tiếp cùng chắn một cung thì bằng nhau, ta suy ra \(\angle EKA=\angle EBD=\angle AKD\to AK\) là phân giác của góc EKD.
b) Tứ giác AIKJ có hai góc đỉnh I, J vuông nên các đỉnh của tứ giác nằm trên đường tròn đường kính AK. Do vậy \(\angle IKA=\angle AJI,\angle JKA=\angle AIJ\to\angle IKA=\angle JKA\) (do tính chất tiếp tuyến). Mà AK là phân giác của góc EKD. Suy ra \(\angle IKE=\angle JDA.\)
c) Gọi T là giao điểm AO với IJ. Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu trong tam giác vuông, ta có
\(AI^2=AT\cdot AO.\) Do chứng minh trên
\(\angle IKA=\angle AJI=\angle AIJ\to\Delta AIH\sim\Delta AKI\left(g.g\right)\to\frac{AI}{AK}=\frac{AH}{AI}\to AI^2=AH\cdot AK.\)
Vậy ta có \(AT\cdot AO=AH\cdot AK\to\frac{AT}{AH}=\frac{AK}{AO}\to\Delta ATK\sim\Delta AKO\to\angle ATH=\angle AKO=90^{\circ}.\) Do đó ta có \(HT\perp AO\), mà \(IJ\perp AO\) do tính chất tiếp tuyến. Suy ra \(TH\equiv IJ\to I,H,J\) thẳng hàng.
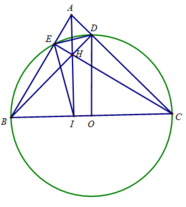

a: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
b: ΔADB vuông tại D có DI là đường cao
nên BD^2=BI*BA