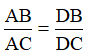Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

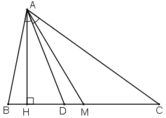
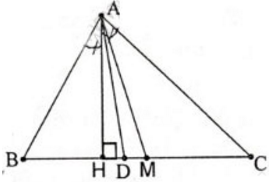
Δ AMB và Δ AMC có: AM chung MB =MC và AC > AB
=> AMC^ > AMB^ => M thuộc CH.(M ở giữa C và H)
AB<AC => B^ > C^ => BAH^ < CAH^ => D thuộc CH.(1)
theo tính chất phân giác:
BD/AB = CD/AC
mà: AC > AB => CD > BD => D thuộc BM (2)
(1) và (2) => D thuộc HM hay D là điểm nằm giữa H và M.

a, ^DAK + ^BAH = 90
^ACH + ^BAH = 90
=> ^DAK = ^ACH
xét tam giác AHC và tam giác AKD có : ^AHC = ^AKD = 90
AH = AK do AHIK là hình vuông (gt)
=> tam giác AHC = tam giác AKD (cgv-gnk)
=> AD = AC (đn)
b, có ADEC là hình bình hành mà ^DAC = 90
=> ADEC là hình vuông (dh) => O là trung điểm của CD (tc)
xét tam giác CAD vuông tại A và tam giác CID vuông tại D
=> AO = CD/2 (đl) và OI = CD/2(đl)
=> AO = OI
=> O thuộc đường trung trực của AI (đl)
có AHIK là hình vuông => HA = HI = KA = KI => H và K thuộc đường trung trực của AI (đl)
=> O;H;K cùng nằm trên đường trung trực của AI
làm nốt ý còn lại của phần b
CEDA là hình vuông (câu b)
=> CD = AE (tc)
OI = CD/2 (cmt)
=> OI =AE/2
xét tam giác AIE
=> tam giác AIE vuông I
=> EI _|_ AI
AI _|_ KO do AHIK là hình vuông (gt)
=> KO // EI (đl)
xét tứ giác KOEI
=> KOEI là hình thang

d) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(AM=\dfrac{20}{2}=10\left(cm\right)\)
Xét ΔAEF có
M\(\in\)AE(gt)
B\(\in\)AF(gt)
\(\dfrac{AM}{ME}=\dfrac{AB}{BF}\left(\dfrac{10}{5}=\dfrac{12}{6}=2\right)\)
Do đó: MB//EF(Định lí Ta lét đảo)
hay BC//EF(Đpcm)
a) Cm \(AD\cdot BC=AB\cdot DC\)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(AD\cdot BC=AB\cdot DC\)(đpcm)

a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành