Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cậu không giải bài giúp tôi thì cũng đừng cmt như thế

a) Xét ΔMAB và ΔMEC có
MA=ME(gt)
ˆAMB=ˆEMCAMB^=EMC^(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔMAB=ΔMEC(c-g-c)

b: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//EC

Cho tam giác ABC vuông tại B , M trên tia đối của t là trung điểm của BC. Trên tia AB lấy E sao cho MA=ME chứng minh rằng
a.Tam giác ABM bằng tam giác ECM
b BC vuông góc với CE
.
a: Xét ΔABM và ΔECM có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔABM=ΔECM
b: Xét tứ giác BACE có
M là trung điểm của BC
M là trung điểm của AE
Do đó: BACE là hình bình hành
Suy ra: CE//AB
hay CE⊥BC

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
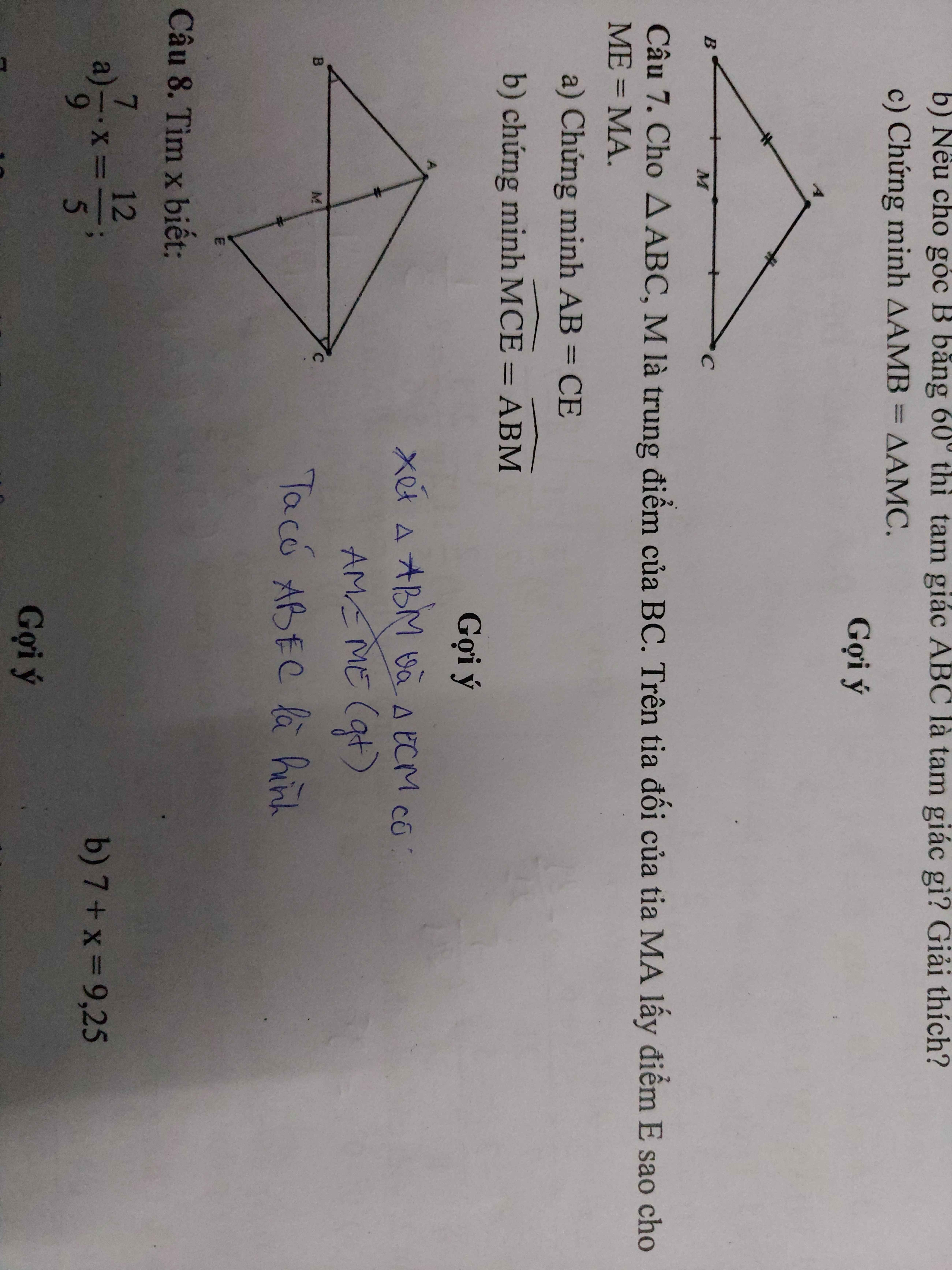
a: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB=CE
b: Ta có: ABEC là hình bình hành
nên AB//CE
hay \(\widehat{MCE}=\widehat{ABM}\)