Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AC//BD

Trả lời:
P/s: Mk chỉ làm đc nhiu đây!!!~^-^
a) Xét tg MAB và tg MDC có:
AM = DM (gt)
MB = MC (suy từ gt)
gAMB = gDMC (đđ)
=> tgMAB = tgMDC (c.g.c)
b) Đề nghị sửa thành: AB = CD và AB // CD.
Vì tgMAB = tgMDC (câu a)
=> AB = CD (2 cạnh tt/ư)
và ABMˆABM^ = DCMˆDCM^( 2 góc t/ư)
mà 2 góc này ở vị trí so l trong nên AB // CD.
c) Nối B với D.
Xét tgAMC và tgDMB có:
AM = DM (gt)
gAMC = gDMB (đđ)
CM = BM (suy từ gt)
=> tgAMC = tgDMB (c.g.c)
=> AC = DB (2 canjht /ư)
Xét tgBAC và tgCDB có:
BA = CD (câu b)
BC chung
AC = DB (c/m trên)
=> tgBAC = tgCDB (c.c.c)
`~Học tốt!~

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác

a) Xét ΔABM và ΔDCM có:
BM=CM(gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
AM=DM(gt)
=>ΔABM=ΔDCM(c.g.c)
b) Vì ΔABM=ΔDCM(cmt)
=>\(\widehat{ABM}=\widehat{DCM}\). Mà hai góc này pử vị trí sole trong
=>AB//DC
c)Xét ΔEBM và ΔFCM có:
\(\widehat{BEM}=\widehat{CFM}=90^o\)
BM=MC(gt)
\(\widehat{BME}=\widehat{CMF}\left(đđ\right)\)
=>ΔEBM=ΔFCM( cạnh huyền-góc nhọn)
=>ME=MF
=>M là trung điểm của EF
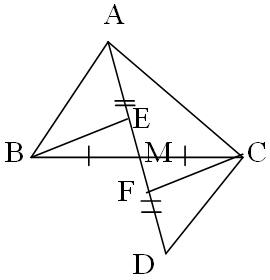
a) Xét ΔABM và ΔDCM, có:
MB = MC (gt)
∠AMB = ∠DCM (đối đỉnh)
MA = MD (gt)
Vậy ΔABM = ΔDCM (c-g-c)
b) Từ ΔABM = ΔDCM (chứng minh câu a)
Suy ra: ∠ABM = ∠ DCM (hai góc tương ứng)
Mà hai góc ∠ABM và ∠DCM ở vị trí so le trong
Vậy AB // DC
c) Xét ΔBEM và ΔCFM (∠E = ∠F = 90º)
Có: MB = MC (gt)
∠AMB = ∠DMC (đối đỉnh)
Do đó: ΔBEM = ΔCFM (cạnh huyền-góc nhọn)
Suy ra: ME = MF (hai cạnh tương ứng)
Vậy M là trung điểm của EF

a ) Xét \(\Delta ABM\)và \(\Delta DCB\) có :
BM = CM (gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
AM = DM (gt)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
Vì : \(\Delta ABM=\Delta DCM\left(cmt\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\) . Mà 2 góc này ở vị trí so le trong
\(\Rightarrow\) AB // DC
c ) Xét \(\Delta EBM\) và \(\Delta FCM\) có :
\(\widehat{BEM}=\widehat{CFM}=90^o\)
BM = MC (gt)
\(\widehat{BME}=\widehat{CMF}\left(đđ\right)\)
\(\Rightarrow\Delta EBM=\Delta FCM\)(cạnh huyền - góc nhọn )
\(\Rightarrow ME=MF\)
\(\Rightarrow M\) là trung điểm của EF ( đpcm)
Chúc bạn học tốt !!!


Bạn tự vẽ hình nha.mk ko bt vẽ trên olm
a) Xét tg AMB và tg DMC có:AM=MD (gt)
MB=MC (gt)
AMB=DMC (2 góc đđ)
nên tg AMB= tg DMC suy ra AB=DC ( cặp cạnh tương ứng),BAM=CDM(cặp góc tương ứng)
b)Xét tg BEM và tg CFM có: BEM=CFM= 90
BM=MC(gt)
EMB=FMC(2 góc đđ)
nên tg BEM= tg CFM(ch-gn) suy ra ME = MF mà M,E,F cùng thược AD
Suy ra M là trung điểm của EF
c) Xét tg BMD và tg CMA có: BM=Cm (gt)
MD=MA (gt)
BMD=CMA (2 góc đđ)
nên tg BMD =tg CMA hay MDB=MAC(cặp góc tương ứng)
mà BAM=CDM(cmt)
nên BAM+MAC=MDB+CDM
hay BAC=CDB