Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

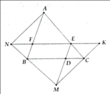
a) Chứng minh được MN//PQ (cùng vuông góc với AC). Chứng minh được MP = QN. Þ ĐPCM.
b) Ta có:
S M N E = 1 2 S M E N C , S N P E = 1 2 S P B N E , S P Q E = 1 2 S , A P E Q S M Q E = 1 2 S Q E M D ⇒ S M N P Q = 1 2 S A B C S .
c) Chu vi MNPQ = MN + PQ + NP + QM
= EC + AE + BE + ED = AC + BE + ED.
Trong tam giác BED, BE + ED ³ BD
Þ Chu vi MNPQ ≥ AC + BD
Þ E là tâm của hình vuông ABCD

a) Xét tứ giác MNCP có
MN // CP(gt)
MP // NC(gt)
\(\Rightarrow\)Tứ giác MNCP là hình bình hành
b) Xét hình bình hành MNCP là hình thoi
\(\Leftrightarrow\)MN=MP
\(\Leftrightarrow\)Tam giác AMN= Tam giác MBP
Xét tam giác AMN và tam giác MBP có
\(\widehat{AMN}\)= \(\widehat{MBP}\)
\(\widehat{BMP}\)= \(\widehat{MAN}\)
Vậy để Tam giác AMN= Tam giác MBP
\(\Leftrightarrow\)AM=MB
Vậy khi M là trung điểm của AB thì MNCP là Hình thoi
c) Hình bình hành MNCP là Hình chữ nhật
\(\Leftrightarrow\)\(\widehat{C}\)=90 độ
\(\Leftrightarrow\)Tam giác ABC vuông tại C
Vậy khi Tam giác ABC vuông tại C thì MNCP là Hình chữ nhật