Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là tâm ngoại tiếp của \(\Delta\)ABC. Ta sẽ chứng minh O thuộc (ATN).
Ta có \(\Delta\)ABC cân tại A có tâm ngoại tiếp O => ^OAC = ^OAB = ^OBA => ^OAT = ^OBN
Ta thấy ^NBM = ^ABC = ^ACB = ^NMB (Do MN // AC) => \(\Delta\)MNB cân tại N => BN = MN
Lại có AN // TM, AT // MN suy ra tứ giác ATMN là hình bình hành => MN = AT
Do đó BN = AT, kết hợp với ^OAT = ^OBN, OA = OB suy ra \(\Delta\)OTA = \(\Delta\)ONB (c.g.c)
=> ^OTA = ^ONB = ^ONA => Bốn điểm O,A,T,N cùng thuộc một đường tròn
Hay đường tròn (ATN) luôn đi qua điểm O cố định (đpcm).

Từ M kẻ \(MH\perp AC\Rightarrow MH=AM.sinA\)
\(S_{AMN}=\dfrac{1}{2}MH.AB=\dfrac{1}{2}AM.AN.sinA\)
Mà góc A cố định \(\Rightarrow S_{min}\) khi \(AM.AN\) đạt min
Qua B, C lần lượt kẻ các đường thẳng song song d, cắt AD tại E và F
\(\Delta BDE=\Delta CDF\left(g.c.g\right)\Rightarrow DE=DF\)
Talet: \(\dfrac{AB}{AM}=\dfrac{AE}{AI}\) ; \(\dfrac{AC}{AN}=\dfrac{AF}{AI}\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AE+AF}{AI}=\dfrac{\left(AD-DE\right)+\left(AD+DF\right)}{AI}=\dfrac{2AD}{AI}\)
Do A; I; D cố định \(\Rightarrow\dfrac{2AD}{AI}\) cố định
\(\dfrac{2AD}{AI}=\dfrac{AB}{AM}+\dfrac{AC}{AN}\ge2\sqrt{\dfrac{AB.AC}{AM.AN}}\Rightarrow AM.AN\ge\dfrac{AB.AC.AI^2}{AD^2}\)
Đẳng thức xảy ra khi và chỉ khi \(\dfrac{AB}{AM}=\dfrac{AC}{AN}\Rightarrow d||BC\) theo Talet đảo
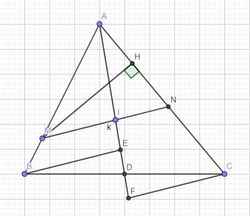
Kẻ \(MI\text{//}AC;DH\bot MN\left(H\in MN\right);IK\bot MN\left(K\in MN\right)\)
\(DHKI\) là hcn \(\Rightarrow DH=IK\Rightarrow S_{DMN}=S_{IMN}\)
Ta có \(\left\{{}\begin{matrix}\Delta AMN\sim\Delta ABC\\\Delta BMI\sim\Delta ABC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\dfrac{S_{AMN}}{S_{ABC}}=\left(\dfrac{AM}{AB}\right)^2\\\dfrac{S_{BMI}}{S_{ABC}}=\left(\dfrac{BM}{AB}\right)^2\end{matrix}\right.\)
\(\Rightarrow\dfrac{S_{AMN}+S_{BMI}}{S_{AB}}=\dfrac{AM^2+BM^2}{AB^2}\ge\dfrac{\dfrac{1}{2}\left(AM+MB\right)^2}{AB^2}\)
\(\Rightarrow\dfrac{S_{ABC}-S_{MNCI}}{S_{ABC}}\ge\dfrac{1}{2}\\ \Rightarrow1-\dfrac{S_{MNCI}}{S_{ABC}}\ge\dfrac{1}{2}\Rightarrow\dfrac{S_{MNCI}}{S_{ABC}}\le\dfrac{1}{2}\\ \Rightarrow S_{MNCI}\le\dfrac{1}{2}S_{ABC}\\ \Rightarrow2\cdot S_{DMN}\le\dfrac{1}{2}S_{ABC}\\ \Rightarrow S_{DMN}\le\dfrac{1}{4}S_{ABC}\)
Dấu \("="\Leftrightarrow AM=MB\Leftrightarrow M\) là trung điểm \(AB\Leftrightarrow N\) là trung điểm AC
Khi đó d đi qua trung điểm AB và AC