Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì ANC = ABD =\(90^O\)Mà chúng ở vị trí đồng vị. \(\Rightarrow\)NC // BD hay CH // BD (đpcm)
vì CH // BD => HCB = CBD ( so le trong )
lại có MBC + MCB = \(90^O\)
BCD + MCB = \(90^O\)
=> MBC = BCD ( cùng phụ với MCB )
Xét tam giác HBC và tam giác DCB có :
MBC = BCD (cmt)
cạnh BC chung
HCB = CBD (cmt)
=> tam giác HBC = tam giác DCB (g - c - g)
=> HBC = BCD ( hai góc tương ứng ) mà chúng ở vị trí so le trong
=> HB // CD (đpcm)

a: Xét ΔBEA và ΔBED có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBEA=ΔBED

hình tự vẽ bn nha a) ta có:tam giác abc vuông tại a => bac = 90 xét tam giác abc có: abc + acb + cab = 180(t/c) mà bac = 90(cmt) ; acb = 36(gt) => 90 +36 + abc = 180 126 + abc = 180 abc= 54
b) ta có: abd = ebd ( vì bd là phân giác của abc) xét tam giác abd và tam giác ebd có: ba=be(gt) ; abd=ebd(cmt) : chung cạnh bd => tam giác abd = tam giác ebd ( c.g.c) (đpcm)
c) ta có: xy vuông góc với ab(gt) => tam giác abk vuông tại b tam giác abc vuông tại a(gt) => ab vuông góc với ac ta có: xy vuông góc với ab (gt) ab vuông góc với ac(cmt) => xy song song với ac(t/c) => bak = abd ( so le trong) xét tam giác abk vuông tại b và tam giác bad vuông tại a có: bak=abd(cmt) ; chung cạnh ba => tam giác abk= tam giác abd ( cgv-gnk) => ak=bd(2 cạnh tương ứng)
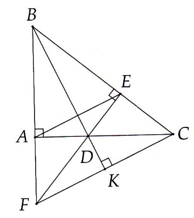

Ta có : BH vuông góc AC (gt)
DC vuông góc AC (gt)
=> BH//DC
C/m tương tự ta được CH//BD