Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AB+ BC =AC nên ba điểm A, B,C thẳng hàng và B nằm giữa A, C
Khi đó C A → . C B → = C A . C B . cos C A → , C B → = 3.5. cos 0 0 = 15.
Chọn B.
Cách khác. Ta có A B 2 = A B → 2 = C B → − C A → 2 = C B 2 − 2 C B → . C A → + C A 2
⇒ C B → C A → = 1 2 C B 2 + C A 2 − A B 2 = 1 2 3 2 + 5 2 − 2 2 = 15.

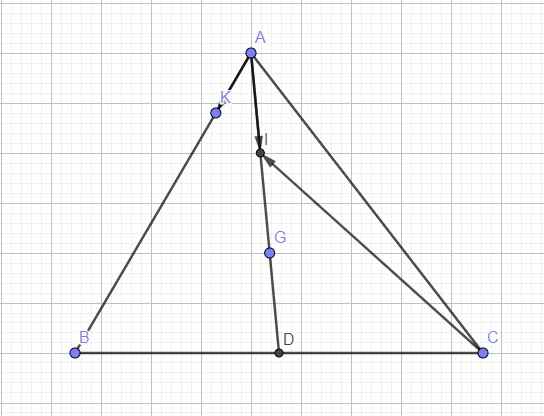
Do G là trọng tâm tam giác
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)



Chọn C.
Ta có: AB + BC = AC nên ba điểm A; B; C thẳng hàng và B nằm giữa A; C
Khi đó
![]()

\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) ; \(\overrightarrow{CB}+\overrightarrow{BA}=\overrightarrow{CA}\) ; \(\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CB}\)
\(\overrightarrow{BA}+\overrightarrow{CB}=\overrightarrow{CA}\) ; \(\overrightarrow{CB}-\overrightarrow{CA}=\overrightarrow{CB}+\overrightarrow{AC}=\overrightarrow{AB}\)
\(\overrightarrow{AB}-\overrightarrow{CA}=\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\) (với M là trung điểm BC)