Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\cos BAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{5-BC^2}{2\cdot1\cdot2}=\dfrac{5-BC^2}{4}\)
\(\Leftrightarrow\dfrac{5-BC^2}{4}=\dfrac{-1}{2}\)
\(\Leftrightarrow5-BC^2=-2\)
\(\Leftrightarrow BC=\sqrt{7}\left(cm\right)\)
b: \(\cos BAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{125-BC^2}{100}\)
\(\Leftrightarrow125-BC^2=50\)
hay \(BC=5\sqrt{3}\left(cm\right)\)
c: \(\cos BAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{7-BC^2}{8\sqrt{3}}\)
\(\Leftrightarrow7-BC^2=4\sqrt{3}\)
hay \(BC=2-\sqrt{3}\left(cm\right)\)

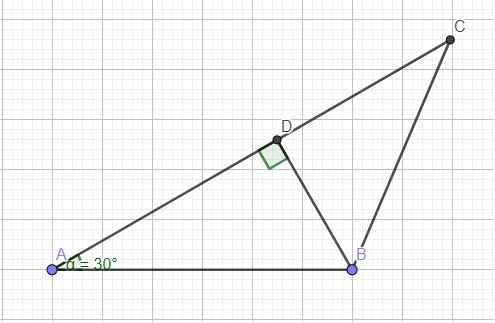
Kẻ đường cao BD (D thuộc AC)
Trong tam giác vuông ABD:
\(cosA=\dfrac{AD}{AB}\Rightarrow AD=AB.cosA=12.cos30^0=6\sqrt{3}\)
\(sinA=\dfrac{BD}{AB}\Rightarrow BD=AB.sinA=12.sin30^0=6\)
\(\Rightarrow CD=AC-AD=8\)
Áp dụng định lý Pitago cho tam giác vuông BCD:
\(BC=\sqrt{BD^2+CD^2}=10\left(cm\right)\)