Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

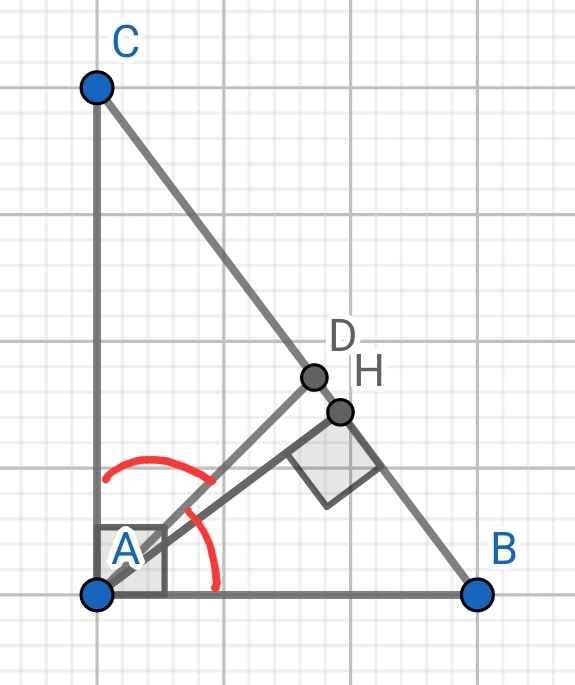
a) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠B = ∠CAH (cùng phụ C)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/HC = HB/AH
⇒ AH.AH = HB.HC
⇒ AH² = HB.HC
Xét hai tam giác vuông: ∆ABC và ∆HAC có:
∠C chung
⇒ ∆ABC ∽ ∆HAC (g-g)
⇒ AC/HC = BC/AC
⇒ AC.AC = HC.BC
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 3² + 4²
= 25
⇒ BC = 5 (cm)
Do AD là tia phân giác của ∠BAC
⇒ BD/CD = AB/AC
⇒ AB/BD = AC/CD
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AB/BD = AC/CD = (AB + AC)/(BD + CD) = (3 + 4)/5 = 7/5
Do AB/BD = 7/5
⇒ BD = AB.5/7 = 3.5/7 = 15/7 (cm)

a: Xét ΔBAE vuông tại A và ΔBHD vuông tại H có
góc ABE=góc HBD
=>ΔBAE đồng dạng với ΔBHD
b: BC=căn 6^2+8^2=10cm
AH=6*8/10=4,8cm

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHAC đồng dạng vói ΔABC
b: \(AB=\sqrt{5^2-3^2}=4\left(cm\right)\)
AH=3*4/5=2,4cm
HB=4^2/5=3,2cm
c: FH/FA=BH/BA
EA/EC=BA/BC
BH/BA=BA/BC
=>FH/FA=EA/EC

a, theo pitago đảo: 212 +282=1225=352 suy ra tam giác ABC vuông
b,theo pitago
AH2=AB2-BH2=AC2-CH2 suy ra 2AH2=AB2+AC2-BH2-CH2
suy ra 2AH2=BC2-BH2-CH2 (Mà BC=BH+CH) suy ra 2AH2=2BHxCH

1: Xét tứ giác AFDE có
\(\widehat{AFD}=\widehat{AED}=\widehat{FAE}=90^0\)
Do đó: AFDE là hình vuông
2: Xét ΔBED vuông tại E và ΔBHA vuông tại H có
\(\widehat{B}\) chung
Do đó; ΔBED∼ΔBHA

a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
b: \(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
=>AC=20(cm)

a) Xét ΔABH vuông tại H và ΔCAH vuông tại H có
\(\widehat{ABH}=\widehat{CAH}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔABH\(\sim\)ΔCAH(g-g)
Suy ra: \(\dfrac{AH}{CH}=\dfrac{BH}{AH}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AH^2=HB\cdot HC\)(đpcm)