Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

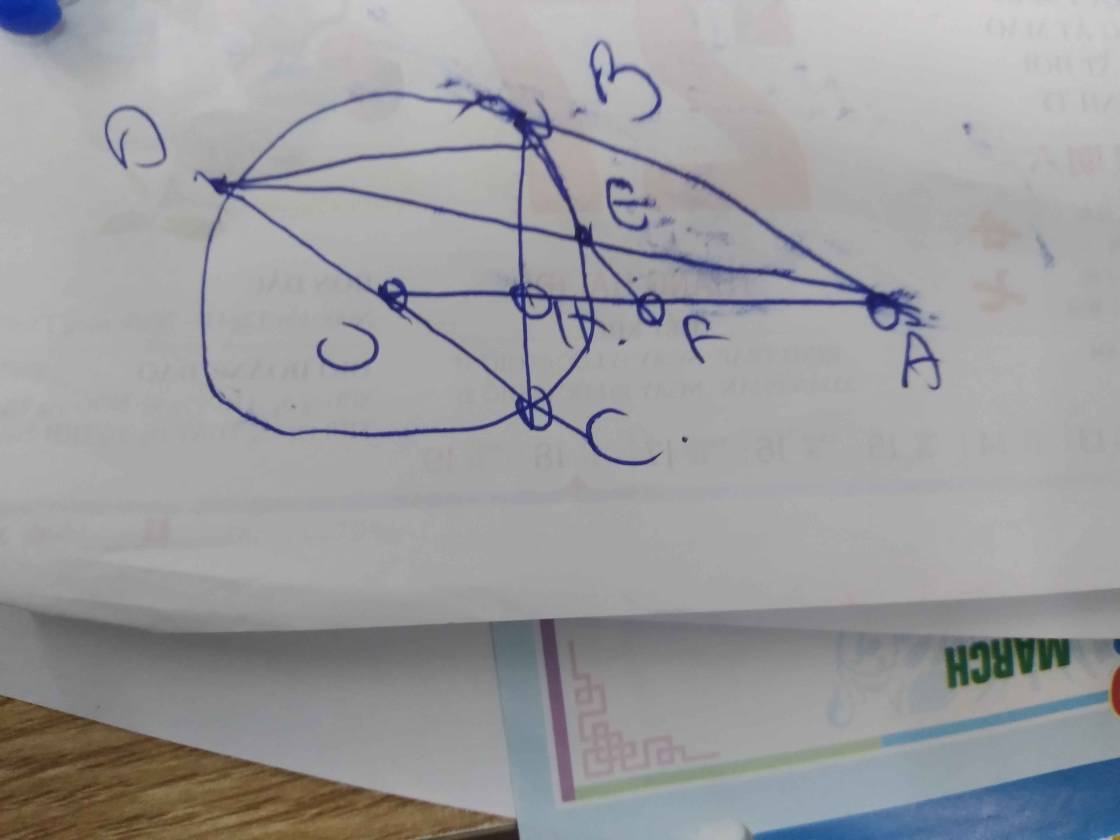
qua B và C kẻ đường // (d) cắt AM tại P & Q => BPCQ là hình bình hành => PM = QM
ta có AB/AE = AP/AN
AC/AF = AQ/AN
=> AB/AE + AC/AF = AP/AN + AQ/AN = ( AM - PM)/AN + ( AM + QM)/AN
= 2AM/AN ( do PM = QM)

gọi D là tiếp điểm của đường tròn (K) trên BC . ta có DB = BE ; CD = CF (tính chất 2 tiếp tuyến cắt nhau)
\(\Rightarrow\) AE = AB + BE = c + BD
AF = AC + CF = b + CD
\(\Rightarrow\) AE + AF = b + c + (BD + CD)
= a + b + c
ta lại có AE = AF (tính chất 2 tiếp tuyến cắt nhau)
\(\Rightarrow\) AE = AF = \(\dfrac{a+b+c}{2}\) (đpcm)
b) BE = AE - AB = \(\dfrac{a+b+c}{2}\) - c = \(\dfrac{a+b-c}{2}\) (đpcm)
c) CF = AF - AC = \(\dfrac{a+b+c}{2}\) -b = \(\dfrac{a+c-b}{2}\) (đpcm)