Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

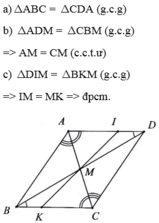
a: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
b: Ta có: ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường
=>MA=MC; MB=MD
c: Xét tứ giác AECN có
AE//CN
AE=CN
Do đó: AECN là hình bình hành
Suy ra: AC cắt EN tại trung điểm của mỗi đường
=>M là trung điểm của EN
hay E,M,N thẳng hàng

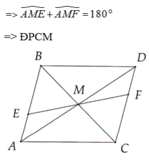
BD cắt AC tại O.
-△ABC=△CDA (g-c-g) \(\Rightarrow AB=DC\)
\(\Rightarrow\)△ABO=△CDO (g-c-g) \(\Rightarrow OA=OC\Rightarrow\)O là trung điểm AC.
-△ABC có: Trung tuyến BO cắt trung tuyến CE tại M.
\(\Rightarrow\)M là trọng tâm của △ABC mà F là trung điểm BC.
\(\Rightarrow\)A,M,F thẳng hàng.