Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: ΔABC\(\sim\)ΔA'B'C' theo tỉ số đồng dạng \(k_1=\dfrac{2}{3}\)
Vì ΔABC\(\sim\)ΔA'B'C' theo tỉ số đồng dạng \(k_1=\dfrac{2}{3}\)
mà ΔA'B'C' \(\sim\)ΔA''B''C'' theo tỉ số đồng dạng \(k_2=\dfrac{3}{4}\)
nên ΔABC\(\sim\)ΔA''B''C'' theo tỉ số đồng dạng \(k_1\cdot k_2=\dfrac{2}{3}\cdot\dfrac{3}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
hay ΔA"B"C"\(\sim\)ΔABC theo tỉ số đồng dạng k=2

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AC^2+AB^2=BC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=26^2-24^2=100\)
hay AC=10(cm)
Áp dụng định lí Pytago vào ΔIMN vuông tại I, ta được:
\(IN^2+IM^2=MN^2\)
\(\Leftrightarrow IM^2=MN^2-IN^2=65^2-25^2=3600\)
hay IM=60(cm)
Ta có: \(\dfrac{AC}{IN}=\dfrac{10}{25}=\dfrac{2}{5}\)
\(\dfrac{AB}{IM}=\dfrac{24}{60}=\dfrac{2}{5}\)
\(\dfrac{BC}{MN}=\dfrac{26}{65}=\dfrac{2}{5}\)
Do đó: \(\dfrac{AC}{IN}=\dfrac{AB}{IM}=\dfrac{BC}{MN}\)
Xét ΔABC và ΔIMN có
\(\dfrac{AC}{IN}=\dfrac{AB}{IM}=\dfrac{BC}{MN}\)(cmt)
Do đó: ΔABC\(\sim\)ΔIMN(c-c-c)

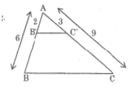
* Cách dựng:
- Trên cạnh AB dựng điểm B' sao cho = 2 cm
- Trên cạnh AC dựng điểm C' sao cho AC' = 3cm
- Nối B'C'
Khi đó AB'C' là tam giác cần dựng
* Chứng minh:
Theo cách dựng, ta có:
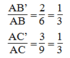
Suy ra: 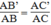
Lại có: ∠ A chung
Vậy △ AB'C' đồng dạng △ ABC (c.g.c)

b: Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(đồng vị, MN//BC)
góc A chung
Do đó: ΔAMN\(\sim\)ΔABC