Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

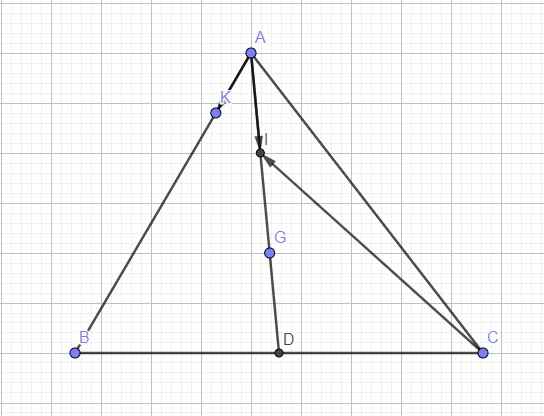
Do G là trọng tâm tam giác
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)

1) Ta có:\(\overrightarrow{AB}+\overrightarrow{DE}-\overrightarrow{DB}+\overrightarrow{BC}=\overrightarrow{AE}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CE}+\overrightarrow{BE}+\overrightarrow{EC}\)
\(=\overrightarrow{AC}+\overrightarrow{BE}+\overrightarrow{CE}+\overrightarrow{EC}=\overrightarrow{AC}+\overrightarrow{BE}\left(đpcm\right)\)2) a) Ta có: \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{ED}+\overrightarrow{BF}+\overrightarrow{FE}+\overrightarrow{CD}+\overrightarrow{DF}\)\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\left(đpcm\right)\)
b) Ta có: \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}\)
\(=\overrightarrow{AD}+\overrightarrow{CB}+\overrightarrow{DB}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{CB}\left(đpcm\right)\)c) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AB}-\overrightarrow{BD}\)
\(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}\)
Ta có: \(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{DB}+\overrightarrow{BC}\) ( đề bài bị lỗi gì à ?? :v ) hay do mình =))

a) \(2\overrightarrow{IA}-\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\Rightarrow2\overrightarrow{IA}-\overrightarrow{IA}-\overrightarrow{AB}+\overrightarrow{IA}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow2\overrightarrow{AI}=\overrightarrow{AC}-\overrightarrow{AB}\Rightarrow\overrightarrow{AB}+2\overrightarrow{AI}=\overrightarrow{AC}\). Từ đó suy ra cách dựng điểm I:
b) Với cách lấy điểm I như trên, ta có điểm I cố định. Khi đó MN đi qua I, thật vậy:
\(\overrightarrow{MN}=2\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=2\overrightarrow{MI}+2\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB}+\overrightarrow{MI}+\overrightarrow{IC}\)
\(=2\overrightarrow{MI}+\left(2\overrightarrow{IA}-\overrightarrow{IB}+\overrightarrow{IC}\right)=2\overrightarrow{MI}\)
Suy ra I là trung điểm MN hay MN đi qua điểm I cố định (đpcm).
c) \(\overrightarrow{MP}=\frac{1}{2}\overrightarrow{MB}+\frac{1}{2}\overrightarrow{MN}=\overrightarrow{MA}+\frac{1}{2}\overrightarrow{MC}\)
Đặt K là điểm sao cho \(\overrightarrow{KA}+\frac{1}{2}\overrightarrow{KC}=\overrightarrow{0}\Rightarrow\hept{\begin{cases}K\in\left[AC\right]\\KA=\frac{1}{2}KC\end{cases}}\)tức K xác định
Khi đó \(\overrightarrow{MP}=\overrightarrow{MK}+\overrightarrow{KA}+\frac{1}{2}\overrightarrow{MK}+\frac{1}{2}\overrightarrow{KC}=\frac{3}{2}\overrightarrow{MK}\), suy ra MP đi qua K cố định (đpcm).