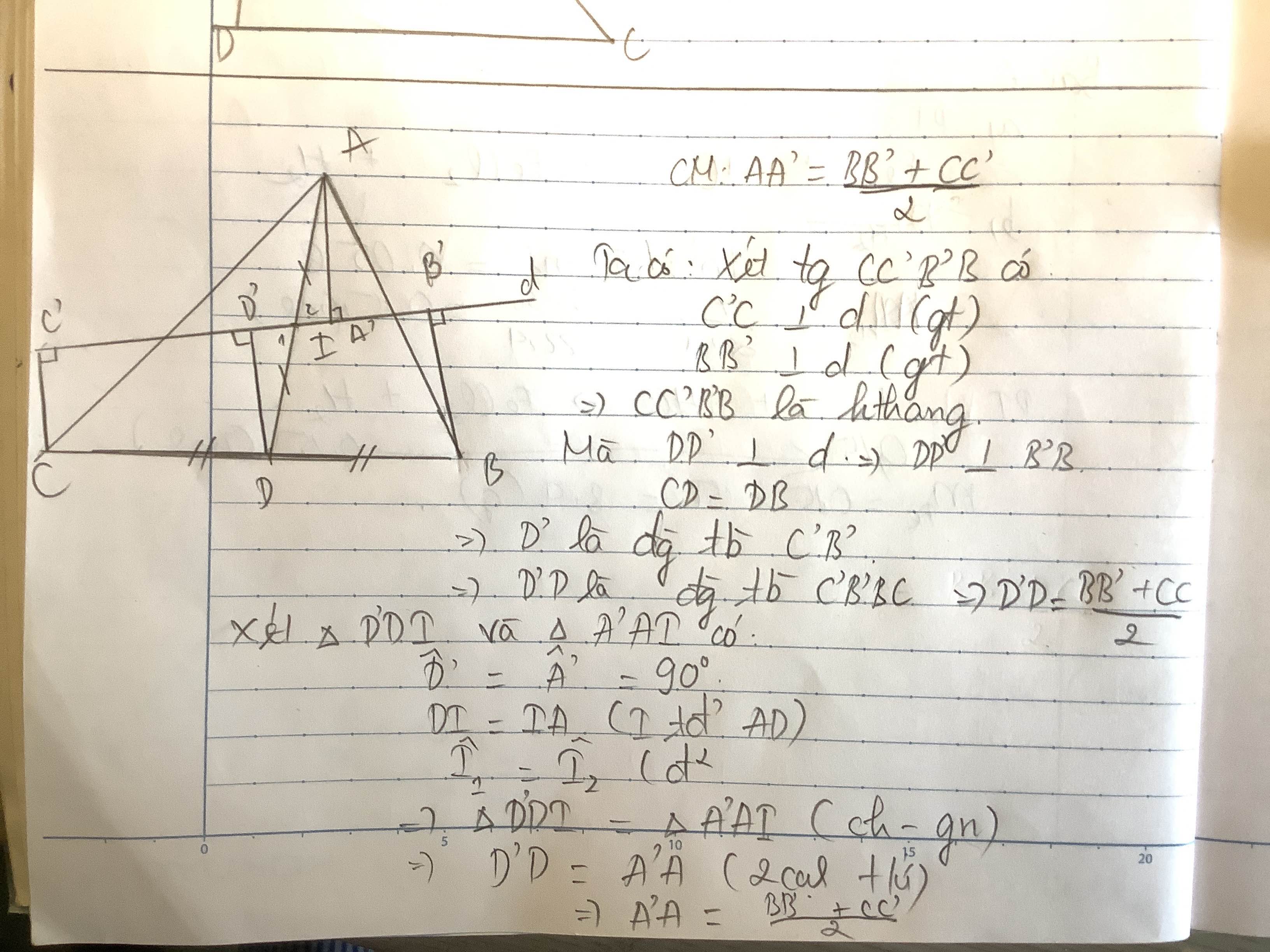Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề là cắt các cạnh AB và AC , ko phải BC và AC
Từ M kẻ MM' \(\perp\) B'C'
Xét tam giác AA'I và tam giác MM'I ( AA'I =MM'I =90) , co :
AIA'=MIM' (đối đỉnh )
AI = IM ( gt)
=> Tam giác AA'I = Tam giác MM'I (c . huyen - gn)
=> AA' = MM'
Xet tg BB'CC' , co :
BB'\(\perp\) B'C'
CC' \(\perp\) B'C'
=> BB' // CC'
=> BB'CC' là hình thang
Ta co :
MM' \(\perp\) B'C'
CC' \(\perp\) B'C'
Ma CC' // BB'
=> MM' // CC' // BB'
Xet hinh thang BB'CC' , co :
MM'//CC' //BB' (cmt)
BM = MC (gt) (1)
=> B'M' = M'C' (2)
Từ (1) vả (2) => MM' là đường trung bình của hình thang BB'CC'
=> MM' =\(\dfrac{CC'+BB'}{2}\)
Mặt khác , ta có : MM' = AA' (cmt)
=> AA' =\(\dfrac{BB'+CC'}{2}\) (dpcm)

Bài 2:
a: Gọi K là trung điểm của DC
Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của DC
Do đó: MK là đường trung bình của ΔBDC
Suy ra: MK//BD và \(MK=\dfrac{BD}{2}\)
hay MK//ID
Xét ΔAMK có
I là trung điểm của AM
ID//MK
Do đó: D là trung điểm của AK
Suy ra: AD=DK
mà DK=KC
nên AD=DK=KC
hay \(AC=AD+DK+DC=3\cdot AD\)
b: Xét ΔAMK có
I là trung điểm của AM
D là trung điểm của AK
Do đó: ID là đường trung bình của ΔAMK
Suy ra: \(ID=\dfrac{MK}{2}\)
hay MK=2ID
mà \(MK=\dfrac{BD}{2}\)
nên \(\dfrac{BD}{2}=2\cdot ID\)
hay \(ID=\dfrac{1}{4}\cdot BD\)

Bài 1:
Gọi E là trung điểm AG và AD là trung tuyến
Mà G là trọng tâm nên \(AE=EG=GD=\dfrac{1}{3}AD\)
Gọi E' và D' lần lượt là hình chiếu của E và D lên d
Ta có AA'//BB'//CC'//DD'//EE'//GG' (cùng vuông góc với d)
Xét hình thang AA'G'G có E là trung điểm AG và EE'//AA'//GG' nên E' là trung điểm A'G'
Do đó EE' là đtb hình thang AA'G'G
Do đó \(EE'=\dfrac{AA'+GG'}{2}\left(1\right)\)
Xét hình thang BB'C'C có D là trung điểm BC và DD'//BB'//CC' nên D' là trung điểm B'C'
Do đó DD' là đtb hình thang BB'C'C
Do đó \(DD'=\dfrac{BB'+CC'}{2}\left(2\right)\)
Xét hình thang EE'D'D có G là trung điểm ED và EE'//DD'//GG' nên G' là trung điểm E'D'
Do đó GG' là đtb hình thang EE'D'D
Do đó \(2GG'=EE'+DD'\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow2GG'=\dfrac{AA'+GG'+BB'+CC'}{2}\)
\(\Rightarrow4GG'=AA'+BB'+GG'+CC'\\ \Rightarrow3GG'=AA'+BB'+CC'\\ \Rightarrow GG'=\dfrac{AA'+BB'+CC'}{3}\)
E sửa lại cái đề đi nha
Kẻ MN đối ME sao cho \(MN=ME\); DE cắt AB tại F
Mà \(AM=MD;\widehat{AMN}=\widehat{EMD}\left(đối.đỉnh\right)\)
Do đó \(\Delta AMN=\Delta DME\left(c.g.c\right)\)
\(\Rightarrow\widehat{ANM}=\widehat{MED};AN=DE\)
Mà 2 góc này ở vị trí so le trong nên AN//DE
Vì tg ABC đều nên \(\widehat{FAD}=60^0;\widehat{ACB}=60^0\)
Mà tg AFD vuông tại F nên \(\widehat{ADF}=90^0-\widehat{FAD}=30^0\)
Do đó \(\widehat{ADF}=\widehat{EDC}=30^0\left(đối.đỉnh\right)\)
Ta có \(\widehat{ECD}=\widehat{ECB}-\widehat{ACB}=90^0-60^0=30^0\Rightarrow\widehat{ECD}=\widehat{EDC}\)
Do đó tg EDC cân tại E nên \(ED=EC\)
\(\Rightarrow EC=AN\)
Ta có AN//DE;DE⊥AB nên AN⊥AB
Vì \(\left\{{}\begin{matrix}\widehat{NAB}=\widehat{ECB}=90^0\\AN=EC\\AB=AC\end{matrix}\right.\) nên \(\Delta ANB=\Delta CEB\left(2.cgv\right)\)
\(\Rightarrow AB=AE\left(1\right);\widehat{NBA}=\widehat{EBC}\\ \Rightarrow\widehat{NBA}+\widehat{ABE}=\widehat{EBC}+\widehat{ABE}=\widehat{ABC}=60^0\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\Delta BNE\) đều
Mà BM là trung tuyến \(\left(NM=ME\right)\) nên cũng là p/g
Vậy \(\widehat{MBE}=\dfrac{1}{2}\widehat{NBE}=30^0\)