Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

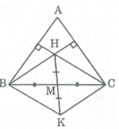
Ta có K là điểm đối xứng của H qua tâm M nên MK = MH
Xét tứ giác BHCK, ta có:
BM = MC (gt)
MK = MH (chứng minh trên)
Suy ra: Tứ giác BHCK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Suy ra: KB // CH, KC // BH
Ta có: CH ⊥ AB (gt)
Suy ra: KB ⊥ AB nên ∠ (KBA) = 90 0
Ta có: BH ⊥ AC (gt)
Suy ra: CK ⊥ AC nên ∠ (KCA) = 90 0

1: Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
2: Ta có: BHCD là hình bình hành
nên Hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của đường chéo BC
nên M là trung điểm của HD
hay H và D đối xứng nhau qua M

1: Xét tứ giác BHCD có
CH//BD
BH//CD
Do đó: BHCD là hình bình hành
2: Ta có: BHCD là hình bình hành
nên Hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HD
hay H và D đối xứng nhau qua M

Xet tứ giác BHCK có
MH=MK; MB=MC => BHCK là hình bình hành (Tứ giác có các cặp cạnh đối cắt nhau tại trung điểm mỗi đường là hbh)
=> CK//BH mà BH vuông góc với AC => CK vuông góc với AC => \(\widehat{ACK}=90^o\)
=> BK//CH mà CH vuông góc với AB => BK vuông góc với AB => \(\widehat{ABK}=90^o\)

a) Xét tứ giác BHCK có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo HK(H và K đối xứng nhau qua M)
Do đó: BHCK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Ta có: BHCK là hình bình hành(cmt)
nên BK//CH và BH//CK(Các cặp cạnh đối trong hình bình hành BHCK)
Ta có: BK//CH(cmt)
nên BK//CF
Ta có: BK//CF(cmt)
CF⊥AB(gt)
Do đó: BK⊥BA(Định lí 2 từ vuông góc tới song song)
Ta có: CK//BH(cmt)
nên CK//BE
Ta có: CK//BE(cmt)
BE⊥AC(gt)
Do đó: CK⊥AC(Định lí 2 từ vuông góc tới song song)
c) Vì H và I đối xứng nhau qua BC
nên BC là đường trung trực của HI
⇔C nằm trên đường trung trực của HI
hay CH=CI(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: BHCK là hình bình hành(cmt)
nên CH=BK(Hai cạnh đối trong hình bình hành BHCK)(2)
Từ (1) và (2) suy ra CI=BK
Gọi O là giao điểm của BC và HI
mà BC là đường trung trực của HI
nên O là trung điểm của HI
Xét ΔHIK có
O là trung điểm của HI(cmt)
M là trung điểm của HK(H và K đối xứng nhau qua M)
Do đó: OM là đường trung bình của ΔHIK(Định nghĩa đường trung bình của tam giác)
⇒OM//IK(Định lí 2 về đường trung bình của tam giác)
hay IK//BC
Xét tứ giác BIKC có IK//BC(cmt)
nên BIKC là hình thang có hai đáy là IK và BC(Định nghĩa hình thang)
Hình thang BIKC(IK//BC) có IC=BK(cmt)
nên BIKC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
a) Xét tứ giác BHCK có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo HK(H và K đối xứng nhau qua M)
Do đó: BHCK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Ta có: BHCK là hình bình hành(cmt)
nên BK//CH và BH//CK(Các cặp cạnh đối trong hình bình hành BHCK)
Ta có: BK//CH(cmt)
nên BK//CF
Ta có: BK//CF(cmt)
CF⊥AB(gt)
Do đó: BK⊥BA(Định lí 2 từ vuông góc tới song song)
Ta có: CK//BH(cmt)
nên CK//BE
Ta có: CK//BE(cmt)
BE⊥AC(gt)
Do đó: CK⊥AC(Định lí 2 từ vuông góc tới song song)
c) Vì H và I đối xứng nhau qua BC
nên BC là đường trung trực của HI
⇔C nằm trên đường trung trực của HI
hay CH=CI(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: BHCK là hình bình hành(cmt)
nên CH=BK(Hai cạnh đối trong hình bình hành BHCK)(2)
Từ (1) và (2) suy ra CI=BK
Gọi O là giao điểm của BC và HI
mà BC là đường trung trực của HI
nên O là trung điểm của HI
Xét ΔHIK có
O là trung điểm của HI(cmt)
M là trung điểm của HK(H và K đối xứng nhau qua M)
Do đó: OM là đường trung bình của ΔHIK(Định nghĩa đường trung bình của tam giác)
⇒OM//IK(Định lí 2 về đường trung bình của tam giác)
hay IK//BC
Xét tứ giác BIKC có IK//BC(cmt)
nên BIKC là hình thang có hai đáy là IK và BC(Định nghĩa hình thang)
Hình thang BIKC(IK//BC) có IC=BK(cmt)
nên BIKC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
