Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

KẺ MK VUÔNG GÓC VỚI AC , MH VUÔNG GÓC VỚI AB.
XÉT TAM GIÁC AMK VÀ TAM GIÁC AMH ( HAI TAM GIÁC VÔNG TẠI K VÀ H ) CÓ :GÓC HAM
AM CHUNG => TAM GIÁC AMK= TAM GIÁC AMH( CẠNH HUYỀN - GÓC NHỌN)
=> AK=AH (1) VÀ MK=MH
XÉT TAM GIÁC HMB VÀ TAM GIÁC KMC ( 2 TAM GIÁC VUÔNG ) CÓ : MK=MH( CMT)
MB=MC ( GT)
=> TAM GIÁC HMB= TAM GIÁC KMC ( ĐỊNH LÝ PY- TA -GO)
=>HB=KC ( 2)
TỪ (1) VÀ (2) TA CÓ : AK+KC = AH+HB
=> AB=AC
=> TAM GIÁC ABC CÂN

Ta có: M là trung điểm của BC
=> BM = CM
Ta có : AM là tia phân giác của góc A
=> Góc BAM = góc CAM
Xét tam giác BAM và tam giác CAM có:
BM = CM (cm trên)
Góc BAM = góc CAM (cm trên)
AM = AM ( cạnh chung)
Vậy tam giác BAM = tam giác CAM (c-g-c)
=> AB = AC ( cạnh tương ứng)
Vậy tam giác ABC là tam giác cân (đpcm)

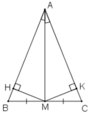
Kẻ MH ⊥ AB, MK ⊥ AC
Xét hai tam giác vuông AHM và AKM, ta có:
∠(AHM) =∠(AKM) = 90o
Cạnh huyền AM chung
∠(HAM) = ∠KAM) (gt)
⇒ ΔAHM = ΔAKM (cạnh huyền, góc nhọn)
Suy ra: MH = MK (hai cạnh tương ứng)
Xét hai tam giác vuông MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 90o
MB = MC ( vì M là trung điểm BC).
MH = MK (chứng minh trên)
⇒ ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.

xét tam giác ABM và tam giác ACM CO
MB=MC
AM CHUNG
GOC M CHUNG
=> TAM GIC ABM = TAM GIÁC AMC
=>AB=AC
=> TAM GIÁC ABC CÂN TẠI A

-Cách 2: -Kẻ MH vuông góc với AB; MK vuông góc với AC( H thuộc AB và K thuộc AC).
-Ta có: tam giác AHM= tam giác AKM( cạnh huyền-góc nhọn).
=> HM=MK. => tam giác BHM= tam giác CKM( cạnh huyền-cạnh góc vuông).
=> góc HBM= góc KCM. => tam giác ABC cân tại A.(đpcm)

Xét tam giác ABM VÀ ACM:
Góc MAB= MAC ( do AM là tia phân giác)
AM: cạnh chung'
BM=BC ( do M là trung điểm BC)
=> tam giác ABM= ACM ( c.g.c)
vậy: AB=AC ( hai cạnh tương ứng)
suy ra: Tam giác ABC là tam giác cân
là tam giác cân
bài này thiếu 1 điều kiện bạn xem lại đi nha
có thêm điều kiện thiếu giải đã khó chứu ko ns đến giải thiếu hẳn ntn.
Bạn xem lại mik làm bài này nhiều nên biết.mik thuộc đề bài mà