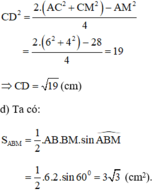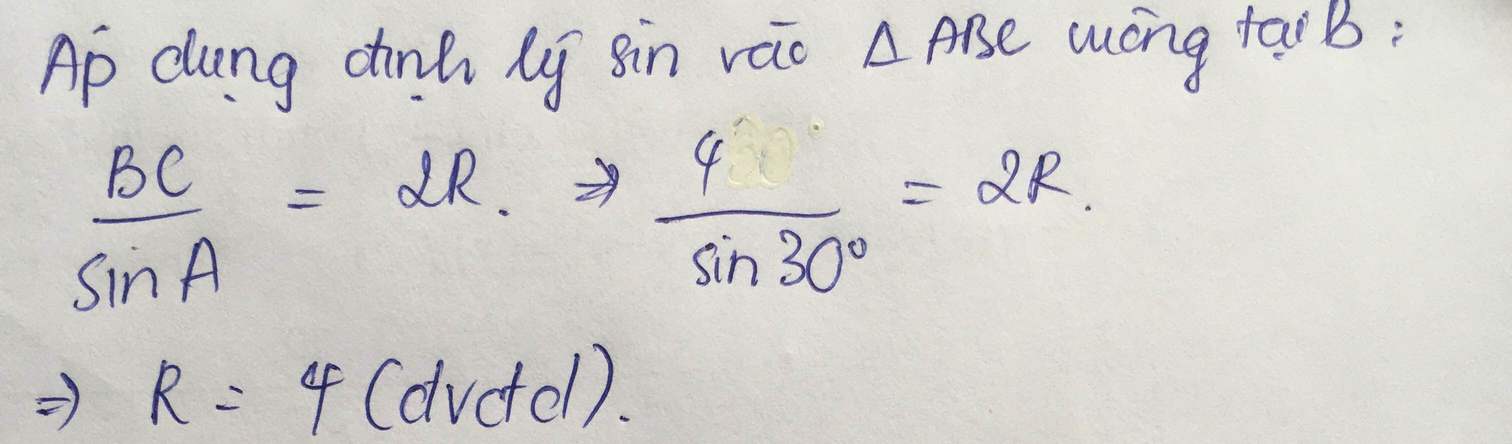Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi G là giao điểm BM và CN. Đặt AB=c, AC=b
Ta có: \(BM^2=\dfrac{2\left(a^2+c^2\right)-b^2}{4}\) ; \(\Rightarrow BG^2=\left(\dfrac{2}{3}BM\right)^2=\dfrac{2\left(a^2+c^2\right)-b^2}{9}\)
\(CN^2=\dfrac{2\left(a^2+b^2\right)-c^2}{4}\Rightarrow CG^2=\dfrac{2\left(a^2+b^2\right)-c^2}{9}\)
Mặt khác \(BG^2+CG^2=BC^2\)
\(\Rightarrow\dfrac{2\left(a^2+c^2\right)-b^2}{9}+\dfrac{2\left(a^2+b^2\right)-c^2}{9}=a^2\)
\(\Rightarrow b^2+c^2=5a^2\)
Áp dụng định lý hàm cos:
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{5a^2-a^2}{2bc}=\dfrac{2a^2}{bc}\Rightarrow bc=\dfrac{2a^2}{cos\alpha}\)
\(S_{ABC}=\dfrac{1}{2}bcsinA=\dfrac{1}{2}.\dfrac{2a^2}{cos\alpha}.sin\alpha=a^2.tan\alpha\)

1.
Gọi $L$ là giao $BM, CN$ thì $L$ là trọng tâm tam giác $ABC$.
Áp dụng công thức đường trung tuyến:
$BM^2=\frac{c^2+a^2}{2}-\frac{b^2}{4}$
$CN^2=\frac{a^2+b^2}{2}-\frac{c^2}{4}$$BL^2=\frac{4}{9}BM^2=\frac{2}{9}(c^2+a^2)-\frac{1}{9}b^2$
$NL^2=\frac{1}{9}CN^2=\frac{1}{18}(a^2+b^2)-\frac{1}{36}c^2$
Theo cong thức Pitago:
$BN^2=BL^2+NL^2$
$\Rightarrow \frac{c^2}{4}=\frac{2}{9}(c^2+a^2)-\frac{1}{9}b^2+\frac{1}{18}(a^2+b^2)-\frac{1}{36}c^2$
$\Rightarrow $5a^2=b^2+c^2$ hay $b^2+c^2=45$
Áp dụng công thức cos:
$a^2=b^2+c^2-2bc\cos A=b^2+c^2-\sqrt{3}bc$
$\Rightarrow 9=45-\sqrt{3}bc\Rightarrow bc=12\sqrt{3}$
$S_{ABC}=\frac{1}{2}bc\sin A=\frac{1}{2}.12\sqrt{3}.\sin 30=3\sqrt{3}$
Đáp án A.
$b=
2.
\(R_{ABC}=\frac{abc}{4S_{ABC}}=\frac{3bc}{4S}=\frac{3.12\sqrt{3}}{4.3\sqrt{3}}=3\)
Đáp án B.

Gọi G là trọng tâm tam giác \(\Rightarrow\) tọa độ G là nghiệm:
\(\left\{{}\begin{matrix}x+7y-10=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow G\left(\dfrac{2}{3};\dfrac{4}{3}\right)\)
Gọi D là trung điểm BC, theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}\Rightarrow\left\{{}\begin{matrix}\dfrac{2}{3}\left(x_D-1\right)=-\dfrac{1}{3}\\\dfrac{2}{3}\left(y_D-3\right)=-\dfrac{5}{3}\\\end{matrix}\right.\) \(\Rightarrow D\left(\dfrac{1}{2};\dfrac{1}{2}\right)\)
Do B thuộc BM nên tọa độ có dạng: \(B\left(10-7b;b\right)\)
Do D là trung điểm BC \(\Rightarrow\left\{{}\begin{matrix}x_C=2x_D-x_B=7b-9\\y_C=2y_D-y_B=1-b\end{matrix}\right.\) \(\Rightarrow C\left(7b-9;1-b\right)\)
Do C thuộc CN nên:
\(7b-9-2\left(1-b\right)+2=0\Rightarrow b=1\)
\(\Rightarrow B\left(3;1\right)\)
Biết tọa độ 2 điểm B; D thuộc BC, bây giờ có thể dễ dàng viết pt BC

1.
Do A không thuộc hai đường trung tuyến đã cho nên giả sử đường trung tuyến xuất phát từ B, C lần lượt là \(2x-y+1=0;x+y-4=0\)
Trọng tâm G của tam giác có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}2x-y+1=0\\x+y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\Rightarrow G=\left(1;3\right)\)
Gọi M là trung điểm BC, ta có \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
\(\Rightarrow\left\{{}\begin{matrix}1+3=\dfrac{2}{3}\left(x_M+2\right)\\3-3=\dfrac{2}{3}\left(y_M-3\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_M=4\\y_M=3\end{matrix}\right.\Rightarrow M=\left(4;3\right)\)
Gọi \(N=\left(m;2m+1\right)\) là trung điểm AC \(\Rightarrow C=\left(2m+2;4m-1\right)\)
Mà C lại thuộc CG nên \(2m+2+4m-1-4=0\Rightarrow m=\dfrac{1}{2}\)
\(\Rightarrow C=\left(3;1\right)\)
Phương trình đường thẳng BC:
\(\dfrac{x-4}{3-4}=\dfrac{y-3}{1-3}\Leftrightarrow2x-y-5=0\)
2.
1.
Trọng tâm G của tam giác có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}x-5y+1=0\\x+y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{2}{3}\end{matrix}\right.\Rightarrow G=\left(\dfrac{2}{3};\dfrac{1}{3}\right)\)
Gọi I là trung điểm BC, ta có \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AI}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2}{3}-1=\dfrac{2}{3}\left(x_I-1\right)\\\dfrac{1}{3}-2=\dfrac{2}{3}\left(y_I-2\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{1}{2}\\y_I=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow I=\left(\dfrac{1}{2};-\dfrac{1}{2}\right)\)
Gọi \(M=\left(5m-1;m\right)\) \(\Rightarrow C=\left(10m-3;2m-2\right)\)
Mà C lại thuộc CN nên \(10m-3+2m-2-1=0\Rightarrow m=\dfrac{1}{2}\)
\(\Rightarrow C=\left(2;-1\right)\)
Phương trình đường thẳng BC:
\(\dfrac{x-2}{2-\dfrac{1}{2}}=\dfrac{y+1}{-1+\dfrac{1}{2}}\Leftrightarrow x+3y+1=0\)

Sửa đề: ΔABC cân tại A
AB=AC
=>1/2AB=1/2AC
=>AN=AM
Xét ΔANC và ΔAMB có
AN=AM
góc NAC chung
AC=AB
=>ΔANC=ΔAMB
=>CN=BM

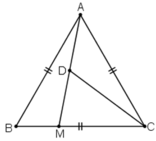
a) Do tam giác ABC là tam giác đều nên 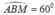 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
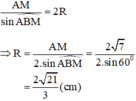
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có: