K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
20 tháng 6 2019
BC < 2AC nếu \(\frac{1}{2}BC=CD< AC\)
Xét hai tam giác ADC có \(\widehat{D_1}=\widehat{G_1}+\widehat{B_1}\).Theo giả thiết \(\widehat{G_1}=90^0\)nên \(\widehat{D_1}\)là góc tù .
Cạnh AC đối diện với \(\widehat{D_1}\) nên là cạnh lớn nhất , Vậy \(AC>DC\)hay \(2AC>2DC=BC\)
5 tháng 8 2019
BC < 2AC nếu \(\frac{1}{2}\)BC = CD < AC
Xét hai tam giác ADC có \(\widehat{D_1}\)=\(\widehat{G_1}\)+\(\widehat{B_1}\).Theo giả thiết \(\widehat{G_1}\)=\(90^o\)nên \(\widehat{D_1}\)là góc tù.
Cạnh AC đối diện với \(\widehat{D_1}\)nên là cạnh lớn nhất. Vậy AC > DC hay 2AC > 2DC = BC
NH
0
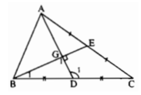
Gọi giao điểm của hai đường thẳng AD và BE là G.
+) Xét tam giác BDG có góc ∠D1 là góc ngoài tam giác nên :
+)Xét tam giác ADC có ∠D1 + ∠A + ∠C = 180º mà ∠D1 > 90º nên ∠D1 là góc lớn nhất trong tam giác đó:
Suy ra: ∠D1 > ∠A
Suy ra: AC > CD ( cạnh đối diện với góc lớn hơn thì lớn hơn ). (1)
+) Mà D là trung điểm của BC nên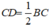
(2)
Từ (1) và (2) suy ra: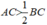
hay 2AC > BC ( điều phải chứng minh )