Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AM vuông góc với DE chứ.
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right);\overrightarrow{DE}=\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{DE}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}.\overrightarrow{AE}-\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AC}.\overrightarrow{AE}\right)\)
\(=\dfrac{1}{2}\left[AB.AE.cos\left(\widehat{BAC}+90^o\right)-AC.AD.cos\left(\widehat{BAC}+90^o\right)-AB.AD.cos90^o+AC.AE.cos90^o\right]\)
\(=0\)
\(\Rightarrow AM\perp DE\)

Gọi giao điểm khác D của hai đường tròn (BED);(CFD) là K'; K'I cắt EF tại L; DL cắt (I;ID) tại M khác D.
Ta thấy IE = IF; AI là phân giác ngoài của ^EAF, từ đây dễ suy ra 4 điểm A,E,I,F cùng thuộc một đường tròn
Vì 3 điểm D,F,E lần lượt thuộc các cạnh BC,CA,AB của \(\Delta\)ABC nên (BED);(CFD);(AFE) đồng quy (ĐL Miquel)
Hay điểm K' thuộc đường tròn (AIFE). Do vậy LI.LK' = LE.LF = LD.LM (= PL/(G) = PL/(I) )
Suy ra 4 điểm K',M,I,D cùng thuộc một đường tròn. Mà ID = IM nên ^IK'D = ^IK'M.
Đồng thời ^DIM = 1800 - ^DK'M = 1800 - ^EK'F + 2.^FK'D = ^BAC + 2.^ACB = 2.^AID
Suy ra IA vuông góc DM, từ đó M,L,D,A thẳng hàng (Vì IA cũng vuông góc AD)
Khi đó dễ thấy AL là phân giác ^BAC, K'L là phân giác ^EK'F, mà tứ giác AEK'F nội tiếp
Suy ra AEK'F là tứ giác điều hòa, từ đây AK' là đường đối trung của \(\Delta\)AEF
Suy ra K' trùng K. Kẻ tiếp tuyến Kx của (G), ta có ^BKx = ^EKx - ^EKB = ^EFK - ^EFD = ^BCK
Do đó (BKC) tiếp xúc với (G) tại K, tức KG đi qua tâm của (BKC) (1)
Gọi S là trung điểm cung lớn BC của (ABC). Có SB = SC và ^BKC = ^AED + ^AFD = 1800 - ^BSC/2
Suy ra S là tâm của đường tròn (BKC) (2)
Từ (1) và (2) suy ra KG luôn đi qua S cố định (Vì S là trung điểm cùng BC lớn cố định) (đpcm).

Tam giác ABC cân tại A, H là trung điểm của BC nên \(AH\perp BC\).
Có \(\overrightarrow{AM}.\overrightarrow{BD}=\dfrac{1}{2}\left(\overrightarrow{AH}+\overrightarrow{AD}\right)\left(\overrightarrow{BH}+\overrightarrow{HD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AH}.\overrightarrow{BH}+\overrightarrow{AH}.\overrightarrow{HD}+\overrightarrow{AD}.\overrightarrow{BH}+\overrightarrow{AD}.\overrightarrow{HD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AH}.\overrightarrow{HD}+\overrightarrow{AD}.\overrightarrow{BH}\right)\) (do \(AH\perp BC\) )
\(=\dfrac{1}{2}\overrightarrow{AH}.\left(\overrightarrow{BH}+\overrightarrow{HD}\right)+\dfrac{1}{2}\left(\overrightarrow{AH}+\overrightarrow{HD}\right).\overrightarrow{BH}\)
\(=\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{BH}+\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{HD}+\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{BH}+\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{BH}\)
\(=\dfrac{1}{2}\overrightarrow{AH}.\overrightarrow{HD}+\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{BH}\) ( do \(AH\perp BC\) )
\(=\dfrac{1}{2}\overrightarrow{HD}\left(\overrightarrow{AH}+\overrightarrow{BH}\right)\)
\(=\dfrac{1}{2}\overrightarrow{HD}\left(\overrightarrow{AH}+\overrightarrow{HC}\right)\) ( doM là trung điểm của BC).
\(=\dfrac{1}{2}\overrightarrow{HD}.\overrightarrow{AC}\)
\(=0\) (Do \(HD\perp AC\) )

a)Xét tam giác BAD và BED(đều là ta giác vuông)
BD là cạnh chung
ABD=DBE(Vì BD là tia p/giác)
\(\Rightarrow\)tam giác BAD=tam giác BED(cạnh huyền góc nhọn)
\(\Rightarrow\)AB=BE(cặp cạnh tương ứng)
b)Vì tam giác BAD=tam giác BED(cạnh huyền góc nhọn)
\(\Rightarrow\)DA=DE(cặp cạnh tương ứng)
Xét tam giác ADF và EDCđều là ta giác vuông)
DA=DE(CMT)
ADF=EDC(đđ)
\(\Rightarrow\)tam giác ADF=tam giác EDC(cạnh góc vuông góc nhọn)
\(\Rightarrow\)DF=DC(cặp cạnh tương ứng)
Do đó tam giác DFC cân tại D(vì DF=DC)
c)Vì DA=DE(CMT)\(\Rightarrow\)tam giác DAE can tại D
Mà ADE=FDC(đđ)
Mà hai tam giác DAE và CDF cân
Do đó:DAE=DEA=DFC=DCF
\(\Rightarrow\)AE//FC vì DFC=DAE

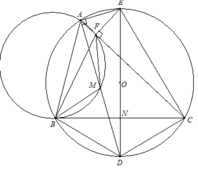
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C