Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

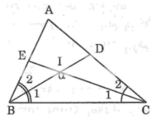
Trong ΔBIC có: ∠(BIC) + ∠B1 + ∠C1 = 180o (tổng 3 góc trong tam giác)
Suy ra: ∠B1 + ∠C1 = 180o - ∠(BIC)
Ta có:
∠B1 = 1/2 ∠B (vì BD là tia phân giác)
∠C1 = 1/2 ∠C (vì CE là tia phân giác)
Suy ra: ∠B + ∠C = 2(∠B1 + ∠C1) = 2.(180o - ∠(BIC))
Trong ΔABC có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠A = 180o - (∠B + ∠C) = 180o - 2.(180o - ∠(BIC)) = 2. ∠(BIC) – 180o
∠(BIC) = α thì ∠A = 2.α – 180o.


b) Xét tam giác ABC có:
BD là đường cao của ABC (gt)
CE là đường cao của ABC (gt)
mà BD cắt CE tại H (gt)
=>AH là đường cao thứ 3
=>AH vuông góc BC
c) Ta có: Tam giác ABC cân tại A (gt)
=> góc ABC = góc ACB = 70o
Xét tam giác ABC CÓ
ABC + ACB + BAC =180 (tổng 3 góc trong tam giác)
70 + 70 + BAC = 180
BAC = 180 - 140 = 40o
Ta có: Tam giác ABC cân tại A, đường cao AH (gt)
=>AH là đường phân giác của BAC
=>BAH = CAH = BAC : 2 =40 : 2= 200
Xét tam giác EAH và tam giác DAH có;
EAH = DAH =200
AH chung
=>EAH = DAH(ch_gn)
=> AHE = AHD=90-20=60o( 2 góc tương ứng)
Ta có: EHD = AHE + AHD = 60 + 60 =1200
=> BHC = EHD =1200 ( 2 góc đối đỉnh)
bang 60