Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc C=180-80-60=40 độ
Vì góc A>góc B>góc C
=>BC>AC>AB
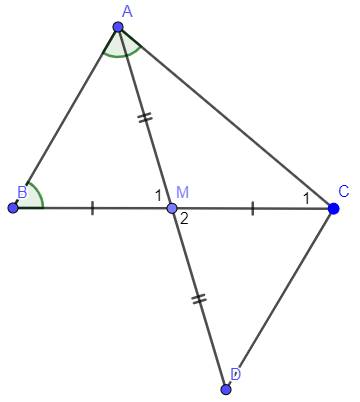
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AB=CD
AB+AC=AB+BD>AD
c: Xét ΔADC có
AN,CM là trung tuyến
AN cắt CM tại K
=>K là trọng tâm
=>CK=2/3CM=2/3*1/2BC=1/3CB
=>BC=3CK

`a)`
`Delta ABC` có :
`hat(BAC)+hat(C_1)+hat(B)=180^0` ( đlý )
hay `80^0+hat(C_1)+60^0=180^0`
`=>hat(C_1)=40^0`
mà `hat(B)>hat(C_1)(60^0>40^0)`
nên `AC>AB`( Qhệ giữa góc và cạnh đối diện trong `Delta` )
`b)`
Có `M` là tđ của `BC`
`=>MB=MC`
Xét `Delta ABM` và `Delta CDM` có :
`{:(AM=DM(GT)),(hat(M_1)=hat(M_2)(đối.đỉnh)),(BM=MC(cmt)):}}`
`=>Delta ABM=Delta CDM(c.g.c)`
`=>AB=CD` ( 2 cạnh t/ứng )(đpcm)

a, Ta có \(\widehat{ABC}+\widehat{ACB}=90^0\Rightarrow3\widehat{ACB}=90^0\Rightarrow\left\{{}\begin{matrix}\widehat{ACB}=30^0\\\widehat{ABC}=60^0\end{matrix}\right.\)
b, Vì \(\left\{{}\begin{matrix}BM=MC\\AM=MD\\\widehat{AMC}=\widehat{BMD}\left(đối.đỉnh\right)\end{matrix}\right.\) nên \(\Delta ACM=\Delta DBM\left(c.g.c\right)\)
c, Vì \(\left\{{}\begin{matrix}AC=BD\left(\Delta ACM=\Delta DBM\right)\\AB.chung\\BC=AD\left(=2AM\right)\end{matrix}\right.\) nên \(\Delta ABC=\Delta BAD\left(c.c.c\right)\)
Do đó \(\widehat{BAC}=\widehat{ABD}=90^0\)
Vậy ...


a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)
a) Theo mối quan hệ giữa cạnh và góc trong tam giác:
\(\widehat{B}>\widehat{C}\Rightarrow AC>AB\)
b) Dễ thấy \(\Delta ABM=\Delta DCM\left(c-g-c\right)\Rightarrow AB=CD\)
Do AC > AB nên AC > CD.
Xét tam giác ACD có AC > CD nên \(\widehat{CDA}>\widehat{CAD}\)
c) Do \(\Delta ABM=\Delta DCM\Rightarrow\widehat{CDA}=\widehat{BAD}\)
Vậy nên \(\widehat{BAM}>\widehat{CAM}\)
Suy ra tia phân giác AJ nằm trong góc BAM hay nằm ngoài góc CAM.